几何意义：积分这个运算涉及两个要素：被积函数和积分区域.曲线积分顾名思义积分区域是空间曲线，而具体的几何或物理意义要根据被积函数而定，如果被积函数f(x，y，z)表示线密度函数，则曲线积分的物理意义就是该曲线物体的质量，特别的，如果f(x，y，z)=1，则曲线积分有明确的几何意义，积分结果就等于曲线的长度.
曲线积分几何意义
原创 | 2023-01-01 16:18:51 |浏览：1.6万
猜你想问
-
匀变速曲线运动匀指的是什么 匀变速运动是速度矢量随时间均匀变化的运动，即单位时间内速度变化量相同，即包括大小相等，更要求方向相同。按照加速度的定义：a=Δv/Δt，单位时间内速度变化量相同，即加... -
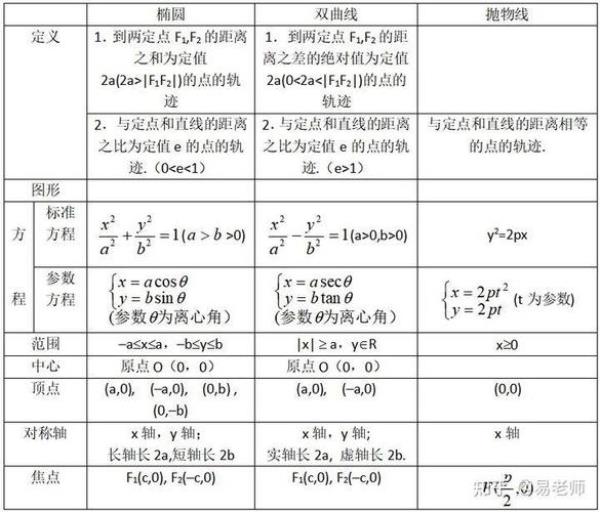圆锥曲线的统一方程 圆锥曲线只有统一极坐标方程p（极径）＝ep／1－eCOSα（P为焦准距）（由e范围对曲线分类）。平面直角坐标系中圆锥曲线有统一定义即PF／d＝e（PF是动点到定点间距离）其中e＞1双曲线，e＝1抛物线，0＜e... -
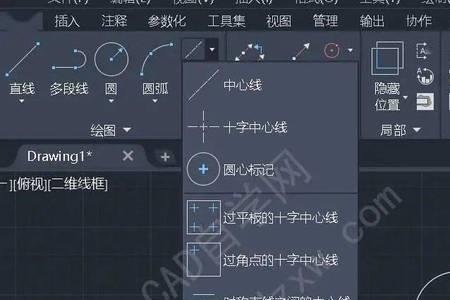cad曲线列表命令 两种方法，方法如下：1、cad中列表菜单的使用，只要在命令行中输入列表命令的快捷键li就可以了，软件会以记事本的形式将图元所包含的信息展现给使用者，当然里面包含着曲线... -
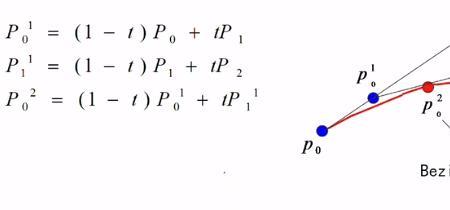贝塞尔曲线几阶方程 答:贝塞尔曲线为n阶方程或n阶函数。第一类贝塞尔函数（Bessel function of the first kind），常简称贝塞尔函数，为贝塞尔方程的第一解。贝塞尔函数的具体形式随方程中任... -
平曲线要素表中缓和曲线怎么看 1，平曲线中的缓和曲线位于该曲线的圆曲线与直线之间。2，平曲线中的缓和曲线超高值由圆曲线向直线部分均匀递减。3，平曲线中的缓合曲线正矢值由圆曲线向直线部分均匀...
