导数的最小值算法

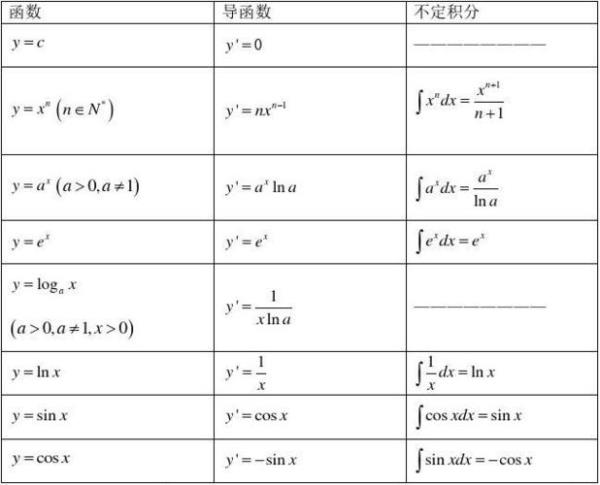
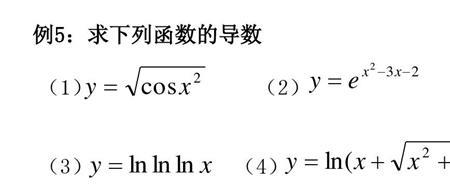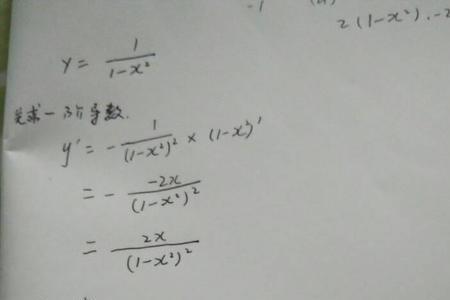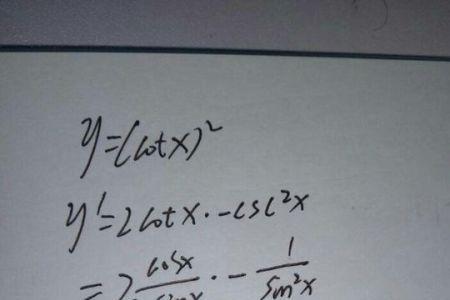f（x）=2^（2x）+2^（-2x）-4（2^x-2^（-x））

令t=2^x-2^（-x），则t^2+2=2^（2x）+2^（-2x），t∈R

∴f（t）=t^2+2-4t

求导f‘（t）=2t-4

当t＜2时，f‘（t）＜0，f（t）单调减

当t=2时，f‘（t）=0，f（t）极小值=-2

当t＞2时，f‘（t）＞0，f（t）单调增

或者直接用二次函数的性质，当t=2时，f（t）最小值=-2

求最小值，需要先求函数的单调区间，标准过程是求导函数f(x)，令f(x) ＝0，解这个方程，容易发现当a的符号不同时，方程的解不同，所以要分类讨论，一般分3类，即a＜0、＝0和＞0，由于前两种情况单调性相同，故可以合并为一种情况，所以最终分两种情况进行讨论：a≤0和a＞0。

导数的最小值算法

先写出导函数，在求导函数=0时候x的值，大于0的部分增，小于0部分单调减，先增后减是极大值，先减后增极小值。再验证极大值(极小值)是不是最大值(极小值)。