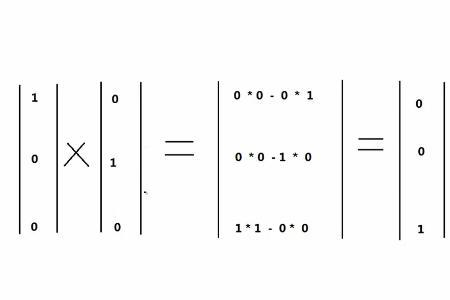列向量与列矩阵的关系:矩阵是一组列(行)向量组成的新的复合向量的展开式。
列矩阵与列向量的区别:
一、性质不同
1、矩阵:是一个按照长方阵列排列的复数或实数集合。
2、向量组:两个及两个以上向量,按照一定的关系集合在一起形成的向量组合,就叫向量组。
二、特点不同
1、矩阵:矩阵的特征值和特征向量可以揭示线性变换的深层特性变换矩阵的行数等于V的维度,变换矩阵的秩等于值域R的维度。
2、向量组:向量组的任意两个极大无关组等价两个等价的线性无关的向量组所含向量的个数相同等价的向量组具有相同的秩,但秩相同的向量组不一定等价。
扩展资料:
矩阵的意义:
1、所有经过变换矩阵后变成了零向量的向量组成的集合,通常用Ker(A)来表示。特别指出的是,核是“变换”(Transform)中的概念,矩阵变换中有一个相似的概念叫“零空间”。
2、如果把V中的任意向量用基的形式写出来,那么这个向量必然也是一部分在核中,另一部分在值域中非零象的原象里。现在对这个向量作变换,核的那部分当然为零了,另一部分的维度刚好等于值域的维度。
3、向量加上加、乘运算构成了空间。向量可以(也能)在空间中变换。使用坐标系(基)在空间中描述向量。
列向量和列矩阵有什么区别
列矩阵又称列向量,是指有一列的矩阵。如果矩阵 A=(aij)m×n只有一行,即m=1,则此时称之为行矩阵,或行向量。
同样,若 A=(aij)m×n只有一列,即n=1,这时称之为列矩阵或列向量。