圆关于直线对称是什么意思

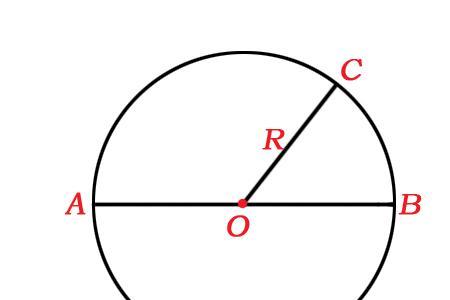
圆关于直线对称，指的是直线为圆的对称轴，也就是直线过圆心，即圆的直径落在对称轴上。其定义是在圆上任取一点A，做这一点关于直线的则对称点B，点B也在圆上，则这个圆就是关于已知直线对称。从图像上看，这条直线就是将圆一分为二，直线的两侧分别是两个半圆。

圆关于直线对称是什么意思

两个圆关于直线对称，则这两个圆应满足两个条件：

1、这两个圆半径相等，是等圆

2、这两个等圆的连心线（即连接两个等圆圆心的线段）被直线垂直且平分。

另外，两等圆的圆心重合并且在直线上，形成同心等圆，这个特殊情况也属于两个圆关于这条直线对称。

圆关于直线对称是什么意思

圆关于直线对称”是指圆“本身”是一个轴对称图形，“关于直线对称再画一个一样的圆”，这种说法是对称圆，是相对于“两个”图形的圆是一种特殊的图形，它既是中心对称图形又是轴对称图形．能用折叠的方法得到圆是一个轴对称图形，其对称轴是任意一条过圆心的直线．