tana=sina/cosa=-1/2
cota=cosa/sina=1/tana=1/(-1/2)=-2
sina/cosa=-1/2
cosa=-2sina
(sina)^2+(cosa)^2=1
代入:
(sina)^2+(-2sina)^2=1
所以:5(sina)^2=1
sina=±√5/5
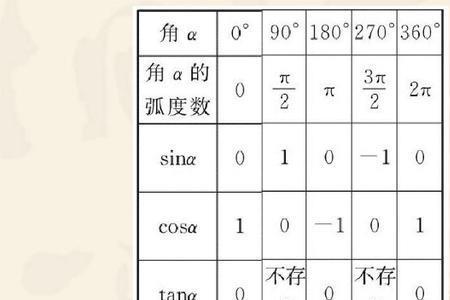
tan负1 /2 角度换算
在一个半径为r的圆中,我们把弧长为半径r的弧所对的圆心角称之为1弧度。
也就说说弧长与半径的比值即是弧度数。
所以圆周所对的弧度数是2πr:r=2π弧度。
1弧度约等于57.3°
1°=π分之一弧度。这里的π=3.14
建立弧度制以后就把角度和实数一一对应了,这样对我们研究数学就方便多了。
2、弧度的公式是否和角度一样?
公式是一样的,只是单位不同,角度制的单位是°,不能省略。而弧度的单位是rad,一半省略不写,所以在看到没有单位的时候肯定是弧度制了。
你在此所说的tanx(弧度)等不等于sinx/cosx(都是弧度)
是对的。因为他们如果用函数表示,可以看成同一个函数,他们有相同的定义域,相同的图像,表达式看上去不一样,其实化简之后是一样的。
3、表示弧度的时候用那种形式呢:
arctan(...)
tan(-1)(....)
-1为角标
tan负1 /2 角度换算
因为tanα= -1/2=-0.5
所以tan(180°-α)=0.5
查三角函数正切值表
180°-α=26°34′,所以,α=153°26′