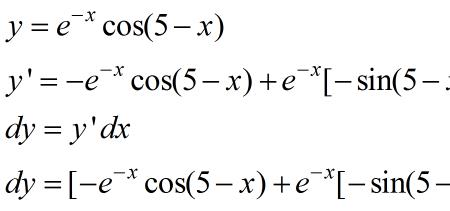x乘以e的负x次方 的原函数是多少求详细过程。
∫xe^(-x)dx=-(x+1)e^(-x)+C。C为积分常数。
分部积分:
∫xe^(-x)dx
=x[-e^(-x)]-∫[-e^(-x)]dx
=-(x+1)e^(-x)+C
分部积分:
(uv)'=u'v+uv'
得:u'v=(uv)'-uv'
两边积分得:∫ u'v dx=∫ (uv)' dx - ∫ uv' dx
即:∫ u'v dx = uv - ∫ uv' d,这就是分部积分公式
也可简写为:∫ v du = uv - ∫ u dv以上只提供参考
x e的负x次方公式
使用分部积分法
∫xe^(-x)dx=-∫x(-e^(-x)dx=-∫xde^(-x)=-{[xe^(-x)-∫e^(-x)dx]}=∫e^(-x)dx-xe^(-x)=-∫e^(-x)d(-x)-xe^(-x)=-e^(-x)-xe^(-x)+C=-(1+x)e^(-x)+c