是 求证:lim(n->∞) sinn/n = 0证明:① 对任意 ε>0 ,∵ |sinn|≤ 1∴要使 | sinn/n - 0| < ε 成立,即只要满足:| sinn/n - 0|=| sinn/n |≤ 1/n < ε,即只要:n > 1/ε 即可.② 故存在 N = [1/ε] ∈N③ 当 n>N 时,④ 恒有:|sinn/n - 0 | < ε 成立.∴ lim(n->∞) sinn/n = 0
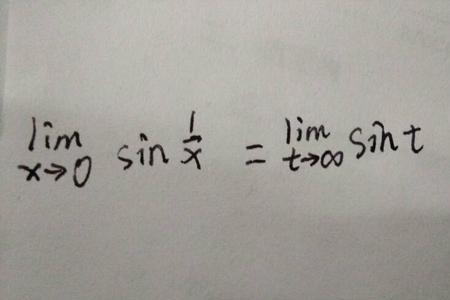
sin n的极限是0的证明
原创 | 2022-12-31 20:32:40 |浏览:1.6万
猜你想问
-
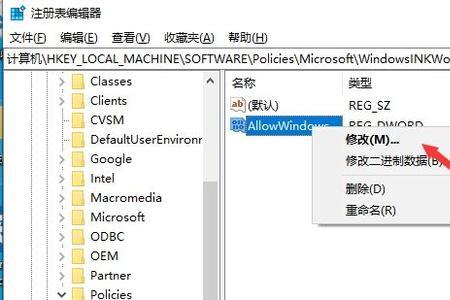 windowsink怎么关掉 1、首先,先来看看Windows Ink功能在哪里显示,对着桌面上任务栏击右键,选择“显示Windows Ink工作区按钮”选项。2、接下来,就会在任务栏托盘图标中看到Windows Ink的...
windowsink怎么关掉 1、首先,先来看看Windows Ink功能在哪里显示,对着桌面上任务栏击右键,选择“显示Windows Ink工作区按钮”选项。2、接下来,就会在任务栏托盘图标中看到Windows Ink的... -
 cousin如何快速记忆 1cousin是堂兄妹的意思2可以拆分成co(前缀,表示共同,一起)➕us我们➕in在……里面3在一个家庭里包括我在内的跟我同辈的关系就是堂兄妹了。...
cousin如何快速记忆 1cousin是堂兄妹的意思2可以拆分成co(前缀,表示共同,一起)➕us我们➕in在……里面3在一个家庭里包括我在内的跟我同辈的关系就是堂兄妹了。... -
 cousin是什么面料 是聚酯纤维面料。1、聚酯纤维由有机二元酸和二元醇缩聚而成的聚酯经纺丝所得的合成纤维。就是俗称的涤纶,被广泛运用于服饰面料。cousin有优良的耐皱性、弹性和尺...
cousin是什么面料 是聚酯纤维面料。1、聚酯纤维由有机二元酸和二元醇缩聚而成的聚酯经纺丝所得的合成纤维。就是俗称的涤纶,被广泛运用于服饰面料。cousin有优良的耐皱性、弹性和尺... -
 cousin和tiger是同类词吗 cousin和tiger不是同类词。You should be friends with your cousin .你应该跟你的表妹和好。I had cousins still living in greece .我有几个亲戚仍住在希腊。I...
cousin和tiger是同类词吗 cousin和tiger不是同类词。You should be friends with your cousin .你应该跟你的表妹和好。I had cousins still living in greece .我有几个亲戚仍住在希腊。I... -
 sim卡信息上报什么意思 意思是指应急信息报送制度,为做好突发事件应急工作中的信息报送工作,规范突发事件信息报告内容、程序和方法,明确信息报告时限和要求,严格信息报告责任追究,确保信息传...
sim卡信息上报什么意思 意思是指应急信息报送制度,为做好突发事件应急工作中的信息报送工作,规范突发事件信息报告内容、程序和方法,明确信息报告时限和要求,严格信息报告责任追究,确保信息传...
