∫secx^2dx=1+∫tanx^2dx=1+∫sinx/(cox^2)(-1)dcosx,然后对后面的部分进行分部积分,即∫sinx/(cox^2)(-1)dcosx=∫sinxd(1/cosx)=sinx / cosx-∫1/cosxdsinx=tanx-1 ,加上前面的1 正好是 tanx。证明完毕。其实可以发现,有sec^2= tanx^2+1,所以在二次方上来回动手脚,徘徊的都是这一个基本公式,做运算时没有用的,只能拆开才能运算下去。
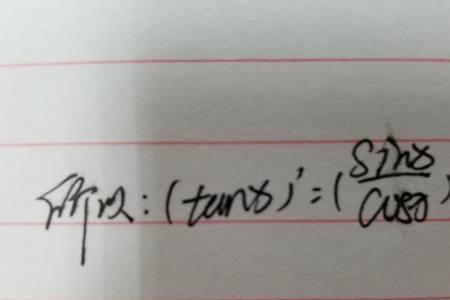
secx的平方为什么等于tanx
原创 | 2022-12-17 17:27:10 |浏览:1.6万
猜你想问
-
 cosx乘secx等于什么 cosx乘secx等于1。这个问题,实际上是要求熟悉同一个角三角函数建立基本关系。三角函数里面基本公式,三角函数的图像与性质,三角函数的变形公式做的比较熟悉,能够灵活...
cosx乘secx等于什么 cosx乘secx等于1。这个问题,实际上是要求熟悉同一个角三角函数建立基本关系。三角函数里面基本公式,三角函数的图像与性质,三角函数的变形公式做的比较熟悉,能够灵活... -
 arcsecx等于什么公式 arccos x=cos-¹arccos表示的是反三角函数中的反余弦。一般用于表示当角度为非特殊角时。由于是多值函数,往往取它的单值,值域为[0,π],记作y=arccosx,我们称它叫做反...
arcsecx等于什么公式 arccos x=cos-¹arccos表示的是反三角函数中的反余弦。一般用于表示当角度为非特殊角时。由于是多值函数,往往取它的单值,值域为[0,π],记作y=arccosx,我们称它叫做反... -
 or与otherwise的区别是什么 or与otherwise的区别是or释义:conj. 或,或者还是要不然n. (Or)人名(中)柯(广东话·威妥玛)(柬)奥(土、匈、土库、阿塞、瑞典)奥尔例句:The mother was pushed into t...
or与otherwise的区别是什么 or与otherwise的区别是or释义:conj. 或,或者还是要不然n. (Or)人名(中)柯(广东话·威妥玛)(柬)奥(土、匈、土库、阿塞、瑞典)奥尔例句:The mother was pushed into t... -
 posses是什么词性 是动词词性,意思是占有,例如:1、Products with dense homogeneous structure posses high corrosion resistance.结构均匀、致密的陶瓷制品耐腐蚀性强。2、Talking o...
posses是什么词性 是动词词性,意思是占有,例如:1、Products with dense homogeneous structure posses high corrosion resistance.结构均匀、致密的陶瓷制品耐腐蚀性强。2、Talking o... -
 为什么苹果se不能更新微信 苹果se的手机机型比较老旧了,首先ios系统已经不给se系列手机更新系统了,也就是说se的系统也是老系统,微信在app store 里面更新的微信版本也是根据手机系统而定的,低...
为什么苹果se不能更新微信 苹果se的手机机型比较老旧了,首先ios系统已经不给se系列手机更新系统了,也就是说se的系统也是老系统,微信在app store 里面更新的微信版本也是根据手机系统而定的,低...
