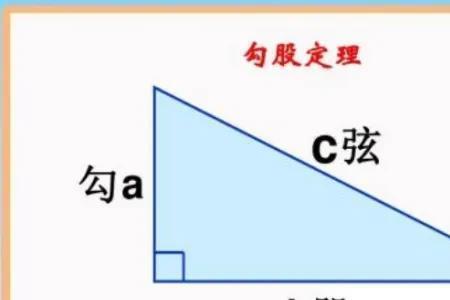
勾股定理指的是直角三角形的两条直边的平方和等于斜边的平方。
勾股定理最早是由商朝的商高发现的。但西方文字记载说是毕达哥拉斯在参加了一个朋友聚会后发现的,其学生为庆祝其发现,宰牛百头,因此,该定理又被称作百牛定理。
该定理在几何学上应用非常广泛。
勾股定理为什么叫百牛定理
原因:在西方有文字记载的最早的证明是毕达哥拉斯给出的。据说当他证明了勾股定理以后,欣喜若狂,宰牛百头,以示庆贺。故西方亦称勾股定理为“百牛定理”
2、勾股定理又叫商高定理、或称毕达哥拉斯定理中国最早的一部数学著作——《周髀算经》的开头,就有这条定理的相关内容:周公问:“窃闻乎大夫善数也,请问古者包牺立周天历度。夫天不可阶而升,地不可得尺寸而度,请问数安从出”商高“数之法出于圆方,圆出于方,方出于矩,矩出九九八十一,故折矩以为勾广三,股修四,径隅五。既方其外,半之一矩,环而共盘。得成三、四、五,两矩共长二十有五,是谓积矩。故禹之所以治天下者,此数之所由生也。”
勾股定理为什么叫百牛定理
国外称勾股定理为毕达哥拉斯定理或百牛定理,原因是:
毕达哥拉斯发现了这个定理后斩了百头牛庆祝,故又称“百牛定理”。