三角形的重心为什么2:1

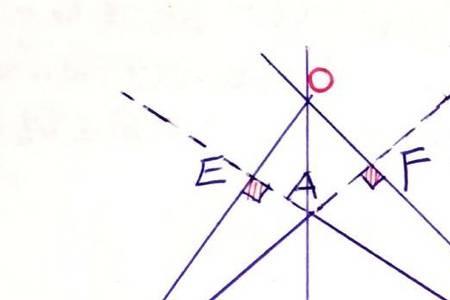
答:三角形三中线的交点叫重心。重心分中线两段的比为2/1。设三角形ABC的中线AD、BE交于G。过E作EF平行BC，交AD于F，E是中点，EF平行BC，∴F是AD的中点，∴EF等_于DC/2，DC=BD∴EF=BD/2，EF平行BC∴三角形BGD相似三角形EGF∴BG/GE=BD/EF，∵BD/EF=2/

1∴BG/GE=2/1。此题得证。

三角形的重心为什么2:1

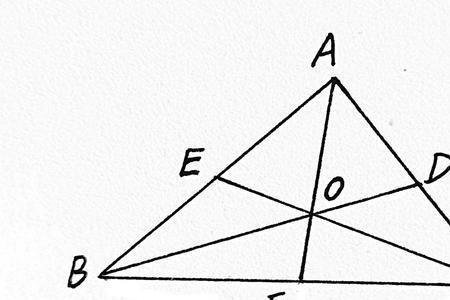
首先重心是三角形中线的交点。 画个三角形ABC，BD和CE分别是中线，相交于F。 连接DE， 然后 DF:FB=DE:BC=1:2 因为DE是中位线。 这个是对任意三角形都不变的定律