解:mxm+1/m=(m一1)的平方+2m一1+1/m=(m一1)的平方+(2m×m一m+1)m,原式=(m一1)的平方+〈2(m一1/4)的平方+3/2〉/m,(m≠0),当m=1时,原式=9/8+3/2=21/8,当m=1/4时,原式=9/16+6=105/16,也就是说此式m∈R,且m≠0,它的最小值是:21/8。

m的平方加m分之一的值
原创 | 2022-12-17 15:08:28 |浏览:1.6万
猜你想问
-
 长虹超白玻璃有4mm的吗 没有长虹玻璃厚度有两个规格5毫米和8毫米,如果是用于门或者淋浴隔断,那么建议选择8毫米厚度会更结实。2、市面上有没钢化和钢化过两种长虹玻璃,钢化过的长虹玻璃会更...
长虹超白玻璃有4mm的吗 没有长虹玻璃厚度有两个规格5毫米和8毫米,如果是用于门或者淋浴隔断,那么建议选择8毫米厚度会更结实。2、市面上有没钢化和钢化过两种长虹玻璃,钢化过的长虹玻璃会更... -
 1cm的钢板能过车吗 那要看跨度有多大,还有汽车有多重才能做定论。四角四个立柱 300×150 型钢当 立柱与大梁 次梁也一样!4米或5米方向你看情况加即可加一根 然后分成了一边各2米宽!中间...
1cm的钢板能过车吗 那要看跨度有多大,还有汽车有多重才能做定论。四角四个立柱 300×150 型钢当 立柱与大梁 次梁也一样!4米或5米方向你看情况加即可加一根 然后分成了一边各2米宽!中间... -
 男生戴10mm的手串合适吗 如果单圈10mm的手串男生戴不会很好看。其实这个还得看男生身高体重而定的,如果男生身高在 175以下体重在130斤左右,手腕还细,那这个尺寸的还勉强可以,但是男生身高在1...
男生戴10mm的手串合适吗 如果单圈10mm的手串男生戴不会很好看。其实这个还得看男生身高体重而定的,如果男生身高在 175以下体重在130斤左右,手腕还细,那这个尺寸的还勉强可以,但是男生身高在1... -
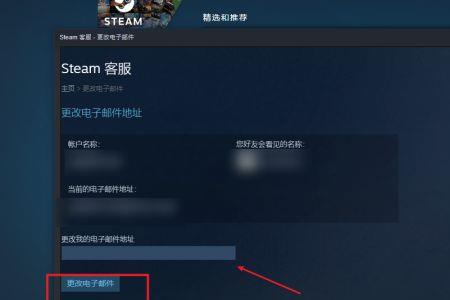 为什么steam的密码一直改不了 回答问题:1、用户密码设置不当,密码不要过长,需要包含一位大写字母,包含小写字母,包含数字。2、改密码入口的问题,前往steam登录界面,点击忘记密码,按照步骤来更改密码。...
为什么steam的密码一直改不了 回答问题:1、用户密码设置不当,密码不要过长,需要包含一位大写字母,包含小写字母,包含数字。2、改密码入口的问题,前往steam登录界面,点击忘记密码,按照步骤来更改密码。... -
 1m的3分之2是什么意思 1米的3分之二,等于2/3(约0.67)米。3分之2是一个分数,它是数的一种表达方式。将一个单位或整体平均分成相同或相等的若干份,取其中的一份或几份叫做分数。3分之2,即将整...
1m的3分之2是什么意思 1米的3分之二,等于2/3(约0.67)米。3分之2是一个分数,它是数的一种表达方式。将一个单位或整体平均分成相同或相等的若干份,取其中的一份或几份叫做分数。3分之2,即将整...
