从角的一边上的一点作角平分线的垂线，使之与另一边相交，则截得一个等腰三角形，垂足为底边上的中点，该角平分线所在直线又成为底边上的中线和高所在直线，可以利用等腰三角形“三线合一”的性质(若题目条件中有垂直于角平分线的线段，则延长该线段止于角的另一边)证题.另外，利用所作的垂直还能构造一对全等的直角三角形.
角分垂等腰归什么意思
原创 | 2022-12-17 14:05:00 |浏览：1.6万
猜你想问
-
荒野大镖客2左下角分别代表什么 两张叠都是用来安装的。如果我没记错，碟上有disk1和disk2。 disk2也是以后启动... 你先插入第一张碟，安装到一半就会提醒你放入下一张碟。因为大镖客2有100g左右，.... -
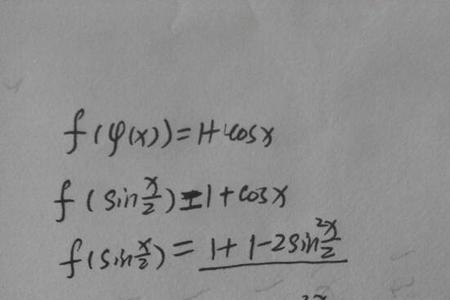半角分是什么意思 半角分是5分的意思。在我国对人民币的说法不同，有很多地区的方言表达不同，但意思是一样的人民币的运算是统一的。我们在生话中都知道1元等于10角，1角等于10分。而有... -
生化危机1-8主角分别是谁 生化危机1的主角是吉尔和克里斯。生化危机2的主角是里昂和卡莱尔，生化危机3的主角是吉尔还有卡洛斯，生化危机4是里昂和艾达，生化危机5是克里斯，夏娃，生化危机6是克里斯... -
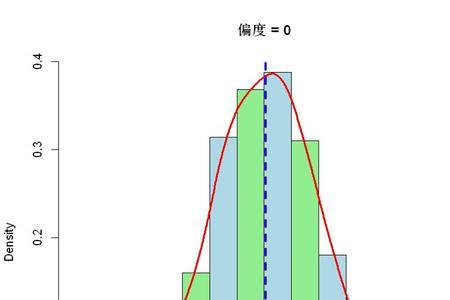三角分布与贝塔分布区别 先说结论，三角分布与贝塔分布区别主要体现在以下几个方面。首先三角分布和贝塔分布的分布面不同，三角分布的范围更加的均匀，所有的材料密度都特别的小。而贝塔分布的... -
庐山恋男女主角分别是谁 男主角郭凯敏、女主角张瑜1980年播出的电影《庐山恋》，饰演男、女主的演员便是郭凯敏和张瑜。他们可以说是，中国内地影视圈的第一对"荧幕CP"。要知道在思想还...
