标准正态分布的公式

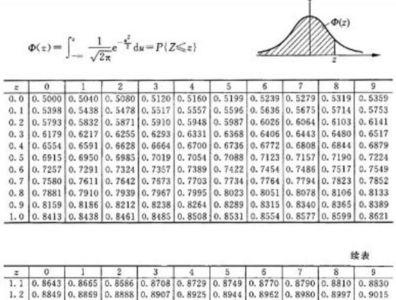
标准正态分布公式为

因为X ～ N(μ， σ^2)， Y =(X- μ)/ σ 所 以

P(x)=(2 π )-^1(/2 )* σ ^- 1( )*exp{[-(x- μ )^2]/(2 σ。^2)}

其中 F(y)为Y 的 分布函数 ，F (x)为X 的分布函数。

而 F(y)=P(Y ≤ y)=P((X -μ)/ σ≤ y)=P(X≤ σy+μ)=Fx( σ所y+以μ)

p(y)=F'(y)=F'x( σ y+μ )* σ =P( σ y+μ )* σ

=[(2 π )^-1(/2)]*e^[- （ y^2)/2]

从而 Y～N(0，1) 。

标准正态分布的公式

正态分布标准化的公式：Y=（X-μ）/σ～N（0，1）。

证明因为X～N（μ，σ^2），所以P（x）=（2π）^（-1/2）*σ^（-1）*exp{[-（x-μ）^2]/（2σ^2）}。

注：F（y）为Y的分布函数，Fx（x）为X的分布函数。

而F（y）=P（Y≤y）=P（（X-μ）/σ≤y）=P（X≤σy+μ）=Fx（σy+μ）。

所以p（y）=F'（y）=F'x（σy+μ）*σ=P（σy+μ）*σ=[（2π）^（-1/2）]*e^[-（x^2）/2]。从而，N（0，1）。正态分布标准化的意义是可以方便计算，是一种统计学概念。