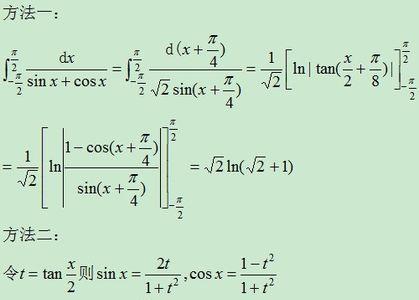∫(1/sint)dt
=∫[sint/(sint)^2]dt
=-∫{1/[1-cost)(1+cost)]}d(cost)
=-(1/2)∫[1/(1-cost)+1/(1+cost)]d(cost)
=-(1/2)∫[1/(1-cost)]d(cost)-(1/2)∫[1/(1+cost)]d(cost)
=(1/2)ln(1-cost)-(1/2)ln(1+cost)+C
=(1/2)ln[(1-cost)/(1+cost)]+C
=(1/2)ln[(1-cost)^2/(sint)^2]+C
=ln|1/sint-cott|+C。
这个函数是不可积的,但是它的原函数是存在的,只是不能用初等函数表示而已。
习惯上,如果一个已给的连续函数的原函数能用初等函数表达出来,就说这函数是“积得出的函数”,否则就说它是“积不出”的函数。比如下面列出的几个积分都是属于“积不出”的函数:
∫e^(-x*x)dx,∫(sinx)/xdx,∫1/(lnx)dx,∫sin(x*x)dx
∫(a*a*sinx*sinx+b*b*cosx*cosx)^(1/2)dx(a*a不等于b*b)
可以证明∫sint/tdt(积分上限为∞,下限为0) =π/2
因为sinx/x是偶函数,所以
∫sint/tdt(积分上限为∞,下限为-∞) =π