单单从计算角度看,一个行列式所有元素都不为零,甚至还可以加上“都为正”的条件,计算出来的行列式(二阶及以上)可为零,这事太常见了。你如果手算过一个二阶行列式,你就能亲见参与计算的数字都不为零(甚至都为正),但算出来零的结果。
从原理上看,一个二阶行列式就是两个列向量为边包围的一个平行四边形的面积,如果这两个列向量都在第一象限,它们的分量就都为正。但如果它们共线了,重叠在了一起(有答说的秩1的情况),它们包围的面积就为零了。这时,行列式的每一个元素都是正的,但行列式还是算出来了零值。
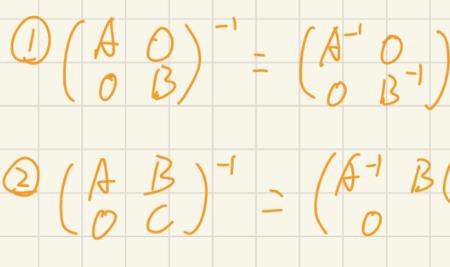
原创 | 2022-12-16 20:40:53 |浏览:1.6万
单单从计算角度看,一个行列式所有元素都不为零,甚至还可以加上“都为正”的条件,计算出来的行列式(二阶及以上)可为零,这事太常见了。你如果手算过一个二阶行列式,你就能亲见参与计算的数字都不为零(甚至都为正),但算出来零的结果。
从原理上看,一个二阶行列式就是两个列向量为边包围的一个平行四边形的面积,如果这两个列向量都在第一象限,它们的分量就都为正。但如果它们共线了,重叠在了一起(有答说的秩1的情况),它们包围的面积就为零了。这时,行列式的每一个元素都是正的,但行列式还是算出来了零值。



Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com