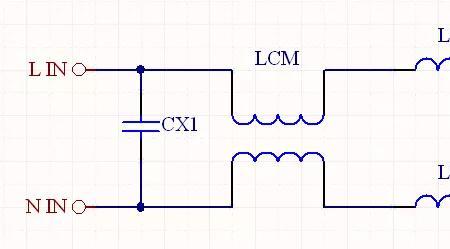
LC滤波电路的时间常数怎么计算
1 .rc振荡回路电容器的电压有:
电压=U*e xp(-t/rc)
U表示电压初值,rc表示电阻电容,t为经过的时间,e xp(-t/rc)表示e的-t/r c次方.时间常数τ=rc,即电容电阻的乘积,引入时间常数后电压=U*e xp(-t/τ)
因此,零输入响应的电压变化是一个指数衰减的过程,理论上是无穷时间,但一般是到3~5个时间常数就认为衰减结束了.
因此放电时间取决于时间常数τ=rc.
2、对于lc振荡回路,情况比较复杂
你只记得于LC的乘积有关就可以了.
要详细的话也麻烦.对一般的L RC回路
按R>2*sqr(L/R)
R=2*sqr(L/R)
R<2 sqr(L/R) sqr(X)表示根号下(X)
分为三种情况,大致地说,放电时间取决于电路中R,L,C的值,U不等于0而I=0时,电容通过L,R放电,解二阶偏微分方程可以得到两个特征值如:p1=-(R/2L)+spr[(R/2L)**(R/2L)-1/LC]p1=-(R/2L)-spr[(R/2L)* (R/2L)-1/L*C]
电容电压=[U/(p2-p1)] [p2exp(p1 t)-p1 exp(p2*t)]
你可以据此分析电容放电时间与L RC的关系.
麻烦的多,因此你只记与LCR的值有关就行了.没有R时就令R=0,因此只于LC的乘积有关了
1 .rc振荡回路电容器的电压有:
电压=U*e xp(-t/rc)
U表示电压初值,rc表示电阻电容,t为经过的时间,e xp(-t/rc)表示e的-t/r c次方.时间常数τ=rc,即电容电阻的乘积,引入时间常数后电压=U*e xp(-t/τ)
lc时间常数什么意思
时间常数是指电容的端电压达到最大值的1/e,即约0.37倍时所需要的时间。在电阻、电容的电路中,它是电阻和电容的乘积。生物膜可以用电容为C和电阻为R的并联等效电路来表示,因而时间常数就是CR,若C的单位是μF(微法),R的单位是MΩ(兆欧),时间常数τ的单位就是秒。在这样的电路中当恒定电流I流过时,时间常数是电容的端电压达到最大值(等于IR)的1—1/e,即约0.63倍所需要的时间,而在电路断开时,时间常数是电容的端电压达到最大值的1/e,即约0.37倍时所需要的时间