两个奇函数的积是奇函数。这是因为这两个奇函数如果自变量取相反数,则各自的函数值也都取相反数。两个负数相乘,结果就是正数。证明过程如下:设有奇函数f(x)和奇函数g(x),则有函数h(x)=f(x)g(x)。而h(-x)=f(-x)g(-x)=[-f(x)][-g(x)]=f(x)g(x)=h(x)。证毕。由函数的奇偶性定义入手就能得到所要的答案。
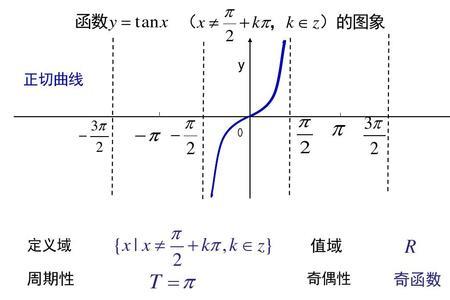
两个奇函数的积是奇函数吗
原创 | 2022-12-06 23:22:10 |浏览:1.6万
猜你想问
-
 两个点一个大是什么字 “头”,现代汉语规范一级字(常用字),普通话读音为tou、tóu,最早见于金文时代,在六书中属于形声字。“头”的基本含义为人身体的最上部分或动物身体的最前的部分,如头骨...
两个点一个大是什么字 “头”,现代汉语规范一级字(常用字),普通话读音为tou、tóu,最早见于金文时代,在六书中属于形声字。“头”的基本含义为人身体的最上部分或动物身体的最前的部分,如头骨... -
 古代形容女子眼睛好看两个字 明眸皓齿:读音为míng móu hào chǐ,释义:明亮的眼睛,洁白的牙齿,形容女子容貌美丽。出自三国魏·曹植《洛神赋》:“丹唇外朗,皓齿内鲜,明眸善睐,靥辅承权。”2,目若秋水:...
古代形容女子眼睛好看两个字 明眸皓齿:读音为míng móu hào chǐ,释义:明亮的眼睛,洁白的牙齿,形容女子容貌美丽。出自三国魏·曹植《洛神赋》:“丹唇外朗,皓齿内鲜,明眸善睐,靥辅承权。”2,目若秋水:... -
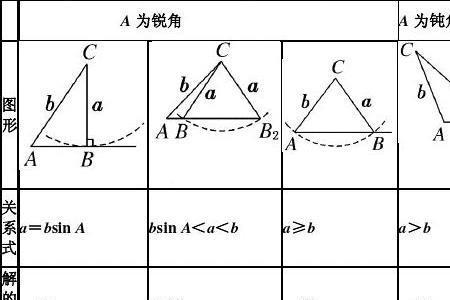 互补的两个角的正弦值相等吗 互补的两个角正弦值是相等的。对的。两角互补,设一个角为α,则另一角为180°-αsinα=sin(180°-α)。诱导公式互补的角正弦值相等,互补的角余弦值互为相反数.互补的角...
互补的两个角的正弦值相等吗 互补的两个角正弦值是相等的。对的。两角互补,设一个角为α,则另一角为180°-αsinα=sin(180°-α)。诱导公式互补的角正弦值相等,互补的角余弦值互为相反数.互补的角... -
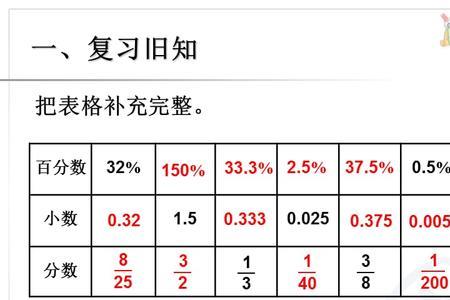 分数是两个整数的比吗 是的。1、分数是指整体的一部分,或更一般地,任何数量相等的部分。2、分数是一个整数a和一个正整数b的不等于整数的比。3、分数表示一个数是另一个数的几分之几,或一...
分数是两个整数的比吗 是的。1、分数是指整体的一部分,或更一般地,任何数量相等的部分。2、分数是一个整数a和一个正整数b的不等于整数的比。3、分数表示一个数是另一个数的几分之几,或一... -
 月升沧海的两个侍卫扮演者 凌不疑身边的两个侍卫的扮演者分别是张琛和孙凯。月升沧海剧中,凌不疑的两个侍卫给这部电视剧提供了不少笑点,而且助推了凌不疑和程少商的感情线路。据了解,在大结局...
月升沧海的两个侍卫扮演者 凌不疑身边的两个侍卫的扮演者分别是张琛和孙凯。月升沧海剧中,凌不疑的两个侍卫给这部电视剧提供了不少笑点,而且助推了凌不疑和程少商的感情线路。据了解,在大结局...
