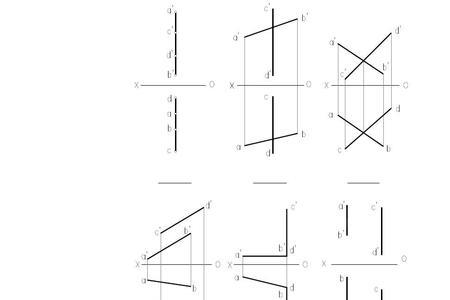
第一种是最常规的做法,列两个方程,然后取值求解。
第二种是建立空间直角坐标系,然后再求需要求法向量的平面的平面方程,然后可以直接看出。
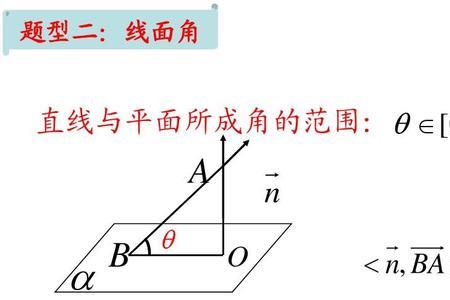
第三种是利用叉乘法,知道平面内相交的两条边的空间向量,就可以利用公式直接套。法向量是空间解析几何的一个概念,垂直于平面的直线所表示的向量为该平面的法向量。由于空间内有无数个直线垂直于已知平面,因此一个平面都存在无数个法向量(包括两个单位法向量)。
空间向量平行于x轴的法向量
x轴的没有法向量,法向量是相对于平面来说的,如可以说垂直x的向量a=(0,0,n),也可以说与x轴平行的向量(m,0,n)。
空间中平面方程的一般形式为:Ax+By+Cz=0。其中x、y、z的系数,A、B、C是平面的法向量的一组方向数,平行于x轴的平面方程的一般形式为:By+Cz+D=0。(0、B、C)是它的一个法向量。