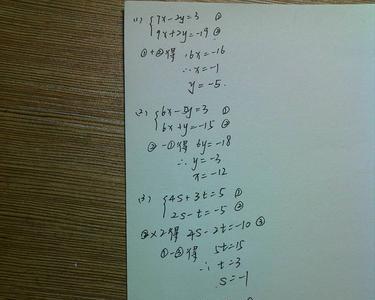二元一次方程化为顶点式过程

二元一次方程化为顶点式的过程

已知一元二次方程一般式为αx^2+bx+c=0(α≠0)，试将这个一元二次方程化为顶点式方程

解:∵αx^2+bx+c=α[x^2+(b/a)x]+c=α[x^2+(b/a)x+(b/2a)^2]+c-α*(b/2α)^2

=α[x+b/(2α)]^2+c-b^2/4α

=α[x+b/(2α)]^2-(b^2-4αc)/4a

∴一元二次方程αx^2+bx+c=0(a≠0)的顶点式方程为:

α[x+b/(2α)]^2-(b^2-4ac)/4a=0。

二元一次方程化为顶点式过程

ax²+bx+c=0（a≠0）x²+（b/a）x+c/a=0x²+（b/a）x+（b/2a）²-（b/2a）²+c/a=0（x+b/2a）²-（b²-4ac）/4a²=0即顶点坐标【-b/2a，-（b²-4ac）/4a²】

二元一次方程顶点公式是X=-b/2a，所有二元一次方程都可化为ax+by+c=0（a、b≠0）的一般式与ax+by=c（a、b≠0）的标准式，否则不为二元一次方程。每个二元一次方程都有无数对方程的解，由二元一次方程组成的二元一次方程组才可能有唯一解，二元一次方程组常用加减消元法或代入消元法转换为一元一次方程进行求解。