正弦和差角公式推导

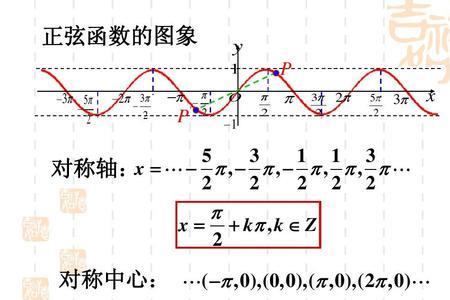
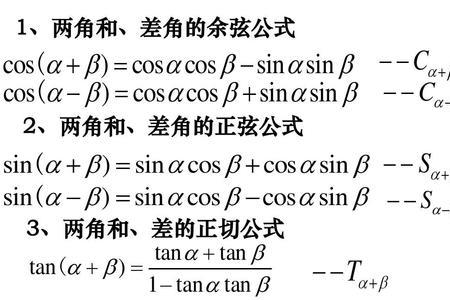先利用单位圆（向量）推到两角和与差的余弦公式，再利用诱导公式推导正弦公式，最后利用同角三角函数的基本关系推到正切公式。

三角函数公式

两角和公式

sin(A+B) = sinAcosB+cosAsinB

sin(A-B) = sinAcosB-cosAsinB

cos(A+B) = cosAcosB-sinAsinB

cos(A-B) = cosAcosB+sinAsinB

tan(A+B) = (tanA+tanB)/(1-tanAtanB)

tan(A-B) = (tanA-tanB)/(1+tanAtanB)

cot(A+B) = (cotAcotB-1)/(cotB+cotA)

cot(A-B) = (cotAcotB+1)/(cotB-cotA

正弦和差角公式推导

可以用向量的方法推出来，在单位圆上任意取两点A(cosa，sina)，B(cosb，sinb)，则向量OA=(cosa，sina)，向量OB=(cosb，sinb)，OA和OB的夹角的余弦值cos(a-b)=OA*OB/(|OA|*|OB|)=cosa*cosb+sina*sinb。

其它的公式可以通过角的恒等变换得到，如sin(a+b)=cos(a-(pi/2-b)))=cosa*cos(pi/2-b)+sina*sin(pi/2-b)=cosa*sinb+sina*cosb