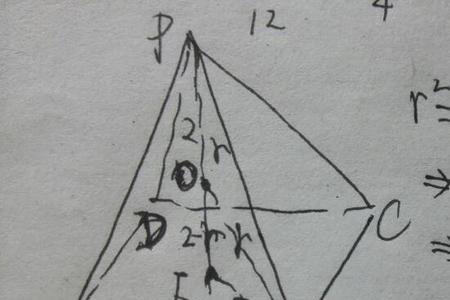
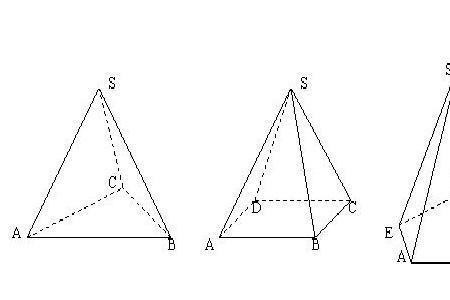
正棱锥底面积为s,高为h,体积公式V=Sh÷3,以锥体顶点为空间坐标原点,锥的高线方向为z轴,建立空间坐标系,要求锥体体积,可以将锥体平行于底面切成无数个小薄饼,每个小薄饼底面面积为s(z),厚度为dz,总体积为:V=∫ s(z)dz
根据底面和截面的关系:s(z)=s₀ z²有:V=∫ s₀z²dz=s₀h/3 (s₀为底面面积,h为高)
对于底面和截面的关系,仍然可以这类地用积分来证明。

原创 | 2022-12-06 22:35:14 |浏览:1.6万
正棱锥底面积为s,高为h,体积公式V=Sh÷3,以锥体顶点为空间坐标原点,锥的高线方向为z轴,建立空间坐标系,要求锥体体积,可以将锥体平行于底面切成无数个小薄饼,每个小薄饼底面面积为s(z),厚度为dz,总体积为:V=∫ s(z)dz
根据底面和截面的关系:s(z)=s₀ z²有:V=∫ s₀z²dz=s₀h/3 (s₀为底面面积,h为高)
对于底面和截面的关系,仍然可以这类地用积分来证明。

Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com