椭圆过焦点垂直于x轴的弦长公式:y²=b²(1-c²/a²)=b²(a²-c²)/a²=b⁴/a²,椭圆弦长公式是一个数学公式,关于直线与圆锥曲线相交求弦长,通用方法是将直线y=kx+b代入曲线方程,化为关于x(或关于y)的一元二次方程,设出交点坐标,利用韦达定理及弦长公式求出弦长。利用圆锥曲线定义及有关定理导出各种曲线的焦点弦长公式就更为简捷。

垂直于x轴的焦点弦公式
原创 | 2022-12-06 22:13:08 |浏览:1.6万
猜你想问
-
 永劫无间开垂直同步会流畅吗 不会!永劫无间垂直同步会掉帧,越高地分辨率需要越好地硬件设备来与之相匹配,从而把画面渲染得更加的清晰,但是在需要在游戏能够流畅运行的条件下来调高分辨率。所以,例...
永劫无间开垂直同步会流畅吗 不会!永劫无间垂直同步会掉帧,越高地分辨率需要越好地硬件设备来与之相匹配,从而把画面渲染得更加的清晰,但是在需要在游戏能够流畅运行的条件下来调高分辨率。所以,例... -
 1660super显卡要开垂直同步吗 是不需要开启的:对于一般用户而言,这个功能没有太大作用,对于高配置的玩家用户来说,用处较大。开启垂直同步后,对显卡消耗挺大的,配置不好的前提下,建议关闭垂直同步功能...
1660super显卡要开垂直同步吗 是不需要开启的:对于一般用户而言,这个功能没有太大作用,对于高配置的玩家用户来说,用处较大。开启垂直同步后,对显卡消耗挺大的,配置不好的前提下,建议关闭垂直同步功能... -
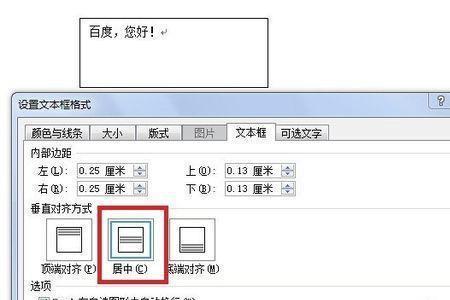 Word里面有垂直居中吗 Word里面有垂直居中,还能水平居中。1、在电脑上打开一个Word文件,点击进行编辑,使用鼠标选中更需要进行编辑居中操作的文字内容,如果是全文,可以通过键盘的【Ctrl】+【...
Word里面有垂直居中吗 Word里面有垂直居中,还能水平居中。1、在电脑上打开一个Word文件,点击进行编辑,使用鼠标选中更需要进行编辑居中操作的文字内容,如果是全文,可以通过键盘的【Ctrl】+【... -
 水泵扬程是垂直高度吗 是垂直高度,垂直高度在水泵上讲叫净扬程,指现场需要将水输送到的高度。因此,水泵的扬程就要满足输送到这个高度的能力,又要克服这个距离中管路的阻力,还要有满足生活或...
水泵扬程是垂直高度吗 是垂直高度,垂直高度在水泵上讲叫净扬程,指现场需要将水输送到的高度。因此,水泵的扬程就要满足输送到这个高度的能力,又要克服这个距离中管路的阻力,还要有满足生活或... -
 扬程是垂直高度吗 答:按照扬程定义,就是垂直高度。不同型号,不同功率,不同粗细的管路都会影响扬程的大小,特别是管路上有弯头,阀门都会使扬程受很大影响,了解了这些因素,在选择水泵时把这...
扬程是垂直高度吗 答:按照扬程定义,就是垂直高度。不同型号,不同功率,不同粗细的管路都会影响扬程的大小,特别是管路上有弯头,阀门都会使扬程受很大影响,了解了这些因素,在选择水泵时把这...
