这是三角函数的不定积分。首先根据cos2x的公式知道sint的平方=(1-cos2t)/2。求∫sint的平方dt等于∫(1-cos2t) /2dt=1/2∫(1-cos2t)dt。常数可以提到∫号外面。∫号里面是两个函数差的积分,它等于两函数积分差。原式=1/2∫dt-1/2∫cos2tdt=1/2t-1/4∫cos2td(2t)+C=1/2t-1/4sin2t+C。
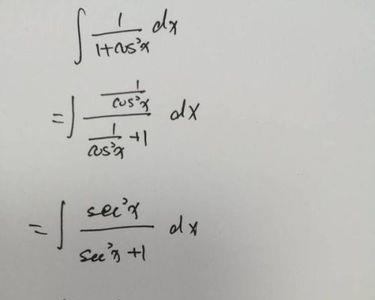
sint的平方不定积分
原创 | 2022-12-06 20:40:41 |浏览:1.6万
猜你想问
-
 sioh4是什么化学名称 Si(OH)4是氢氧化硅的化学式,一般叫做原硅酸或正硅酸(H4SiO4),化学物质,二氧化硅(SiO2)的水合物。H4SiO4不稳定,容易分解成为硅酸(H2SiO3)。盐酸和Na2SiO3溶液起反应时生成白...
sioh4是什么化学名称 Si(OH)4是氢氧化硅的化学式,一般叫做原硅酸或正硅酸(H4SiO4),化学物质,二氧化硅(SiO2)的水合物。H4SiO4不稳定,容易分解成为硅酸(H2SiO3)。盐酸和Na2SiO3溶液起反应时生成白... -
 h2sio3是什么化学名 是硅酸。硅酸是一种无机物,化学式为h2sio3。是一种弱酸,它的盐在水溶液中有水解作用。游离态的硅酸,包括原硅酸(H4SiO4)、偏硅酸(H2SiO3)、二硅酸 (H2Si2O5),酸性很弱。...
h2sio3是什么化学名 是硅酸。硅酸是一种无机物,化学式为h2sio3。是一种弱酸,它的盐在水溶液中有水解作用。游离态的硅酸,包括原硅酸(H4SiO4)、偏硅酸(H2SiO3)、二硅酸 (H2Si2O5),酸性很弱。... -
 h 2sio 3的用途有哪些 H2SiO3是硅酸的化学式,一种弱酸,它的盐在水溶液中有水解作用。将过饱和的硅酸溶液长期放置,会有无定形的二氧化硅沉淀,为乳白色沉淀,并以胶态粒子、沉淀物或凝胶出现。...
h 2sio 3的用途有哪些 H2SiO3是硅酸的化学式,一种弱酸,它的盐在水溶液中有水解作用。将过饱和的硅酸溶液长期放置,会有无定形的二氧化硅沉淀,为乳白色沉淀,并以胶态粒子、沉淀物或凝胶出现。... -
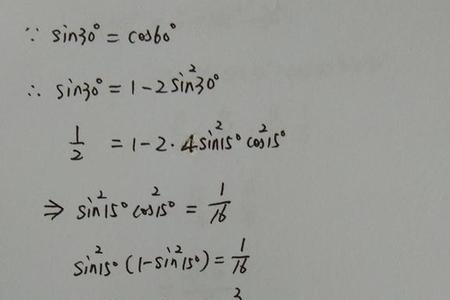 sincos的积分怎么求 sinxcosx的不定积分是sinxcosxdx=∫sinxdsinx=(sin²x)/2+C,一个函数,可以存在不定积分,而不存在定积分也可以存在定积分,而不存在不定积分。 一个连续函数,一定...
sincos的积分怎么求 sinxcosx的不定积分是sinxcosxdx=∫sinxdsinx=(sin²x)/2+C,一个函数,可以存在不定积分,而不存在定积分也可以存在定积分,而不存在不定积分。 一个连续函数,一定... -
 psi用的什么手机 psi用的是ROG游戏手机5。ROG游戏手机5有暗影黑和幻影白两种配色,给人一种克制而又蕴藏着蓬勃力量的观感。既然是游戏手机,不得不提到其大尺寸的ROG logo灯,基于炫彩...
psi用的什么手机 psi用的是ROG游戏手机5。ROG游戏手机5有暗影黑和幻影白两种配色,给人一种克制而又蕴藏着蓬勃力量的观感。既然是游戏手机,不得不提到其大尺寸的ROG logo灯,基于炫彩...
