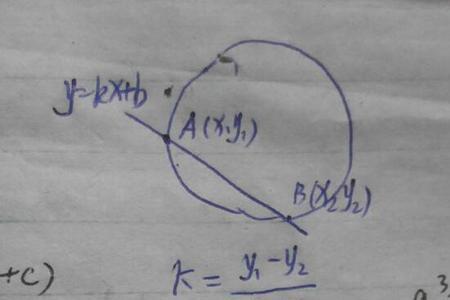
方法:焦点弦,A(x1,y1),B(x2,y2),AB为椭圆的焦点弦,M(x,y)为AB中点,则L=2a±2ex设直线与椭圆交于P1(x1,y1),椭圆弦长公式 若直线过焦点并知道倾斜角 ,则还可以使用 推导 设直线y=kx+b 代入椭圆的方程可得:x/a+ (kx+b)/b=1,设两交点为A、B,点A为(x1,y1),弦长=│x1x2│√(k^2+1)=│y1y2│√[(1/k^2)+1] 其中k为直线斜率,(x1,y1),(x2,y2)为直线与曲线的两交点.。
直线与椭圆相交的弦长公式
如下图: 方法: 焦点弦,A(x1,y1),B(x2,y2),AB为椭圆的焦点弦,M(x,y)为AB中点,则L=2a±2ex
设直线与椭圆交于P1(x1,y1),P2(x2,y2),且P1P2斜率为k,则 平面内到定点F1、F2的距离之和等于常数(大于|F1F2|)的动点P的轨迹,F1、F2称为椭圆的两个焦点。其数学表达式为:|PF1|+|PF2|=2a(2a>|F1F2|)。