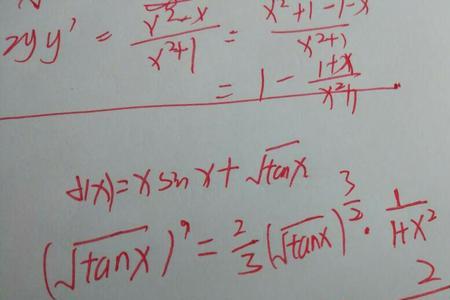sinx^2的导数是sin2x。
1、这是一个复合函数的求导问题,先求外函数y=(sinx)^2即2sinx,再求内函数sinx的导即cosx,故(sinx)^2的导数为2sinxcos也就是sin2x,[(sinx)^2]'=2(sinx)(sinx)'=2sinxcosx=sin2x,所以(sinx)^2的导数为sin2x,(sin2x)'=2cos2x。
2、sinx^2的原函数是x/2-(1/4)sin2x+C,其中C为常数,sin指正弦函数在直角三角形中任意一锐角∠A的对边与斜边的比叫作∠A的正弦,记作sinA即sinA=∠A的对边/斜边,古代说的勾三股四弦五中的弦,就是直角三角形中的斜边,勾、股是直角三角形的两条直角边。
3、倍角公式是三角函数中非常实用的一类公式,就是把二倍角的三角函数用本角的三角函数表示出来,在计算中可以用来化简计算式、减少求三角函数的次数,在工程中也有广泛的运用,倍角公式是三角函数中非常实用的一类公式。
sinx^2导数
sin²x
=(sinx)²
=2sinx(sinx)'
=2sinxcosx
=sin2x
函数可导的条件:
如果一个函数的定义域为全体实数,即函数在其上都有定义。函数在定义域中一点可导需要一定的条件:函数在该点的左右导数存在且相等,不能证明这点导数存在。只有左右导数存在且相等,并且在该点连续,才能证明该点可导。
可导的函数一定连续连续的函数不一定可导,不连续的函数一定不可导