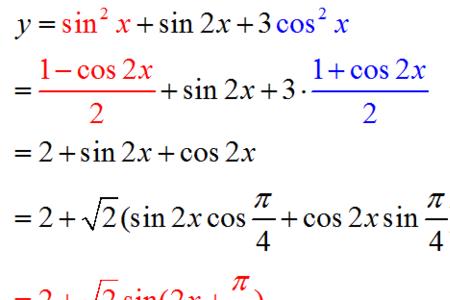cos三次方x怎么算

{cos^3 (3x)}'

= 3 cos^2(3X) {cos(3x)}'

= 3 cos^2(3X) {-sin(3x)} (3x)'

= 3 cos^2(3X) {-sin(3x)} 3

= -9 sin(3x) cos^2(3x)

扩展资料：

可导，即设y=f(x)是一个单变量函数， 如果y在x=x0处左右导数分别存在且相等，则称y在x=x[0]处可导。如果一个函数在x0处可导，那么它一定在x0处是连续函数。

函数可导的条件：

如果一个函数的定义域为全体实数，即函数在其上都有定义。函数在定义域中一点可导需要一定的条件：函数在该点的左右导数存在且相等，不能证明这点导数存在。只有左右导数存在且相等，并且在该点连续，才能证明该点可导。

可导的函数一定连续连续的函数不一定可导，不连续的函数一定不可导。

cos三次方x怎么算

cosx三次方积分如下：

∫cos³xdx=∫cos²xd(sinx)=∫(1-sin²x)d(sinx)

=sinx-(1/3)sin³x+常数