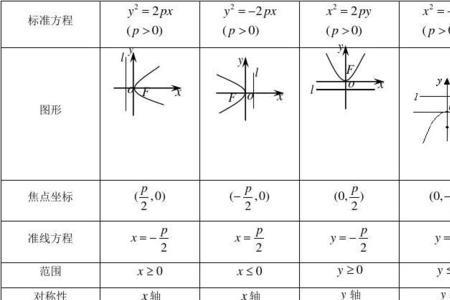
抛物线关于x轴、y轴、原点、顶点对称的抛物线的解析式。
二次函数图像的对称一般有四种情况:可以用一般式或顶点式表达,分别是:
1. 关于x轴对称,y=ax+bx+c关于x轴对称后,得到的解析式是y=-ax-bx-cy=a(x-h)+k关于x轴对称后,得到的解析式是y=-a(x-h)-k.
2. 关于y轴对称,y=ax+bx+c 关于y轴对称后,得到的解析式是y=ax-bx+cy=a(x-h)+k关于y轴对称后,得到的解析式y=a(x+h)+k。
3. 关于原点对称,y=ax+bx+c关于原点对称后,得到的解析式是y=-ax+bx-cy=a(x-h)+k关于原点对称后,得到的解析式是y=-a(x-h)+k
4. 关于顶点对称, y=ax+bx+c关于顶点对称后,得到的解析式是y=-ax-bx+c-b/2ay=a(x-h)+k关于顶点对称后,得到的解析式是y=-a(x-h)+k.
需要注意的是,对于以上四种对称要在结合开个方向、对称轴的位置以及与y轴的交点三个方面结合图像理解记忆。而对于抛物线关于定点对称问题我们一般都是化成顶点式再变换。掌握抛物线的四种对称方式,理解公式的推导过程。