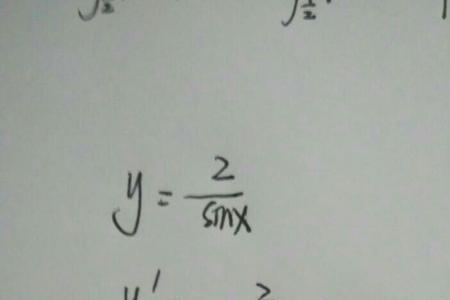y的三阶导数=y的二阶导数
设y的二阶导数为z
也就是z的导数=z
所以z=e^x+c
也就是y的二阶导数=e^x+c
所以y=e^x+ax^2+bx+c
a,b,c为任意常数
如果函数y=f(x)在开区间内每一点都可导,就称函数f(x)在区间内可导。这时函数y=f(x)对于区间内的每一个确定的x值,都对应着一个确定的导数值,这就构成一个新的函数,称这个函数为原来函数y=f(x)的导函数。
函数y=f(x)在x0点的导数f'(x0)的几何意义:表示函数曲线在点P0(x0,f(x0))处的切线的斜率(导数的几何意义是该函数曲线在这一点上的切线斜率)。