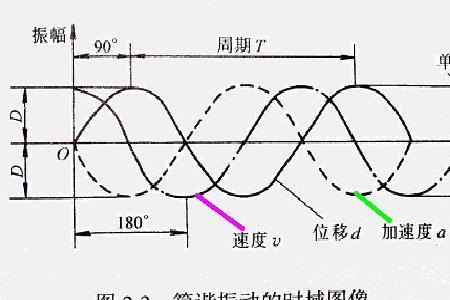
在绘制根轨迹图时,我们没有求传递函数的相位和幅值,因此不是频域分析方法。
另一方面,根轨迹分析不同增益K下的特征方程,我们之所以在复频域解特征方程而不是在时域内求解,是因为拉普拉斯变换能将时域微分方程转化为代数方程,极大方便了数学计算,但这个过程的哲学思想还是基于时域微分方程的,所以跟轨迹分析是时域分析方法的一种。
原创 | 2022-12-05 19:32:15 |浏览:1.6万
在绘制根轨迹图时,我们没有求传递函数的相位和幅值,因此不是频域分析方法。
另一方面,根轨迹分析不同增益K下的特征方程,我们之所以在复频域解特征方程而不是在时域内求解,是因为拉普拉斯变换能将时域微分方程转化为代数方程,极大方便了数学计算,但这个过程的哲学思想还是基于时域微分方程的,所以跟轨迹分析是时域分析方法的一种。



Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com