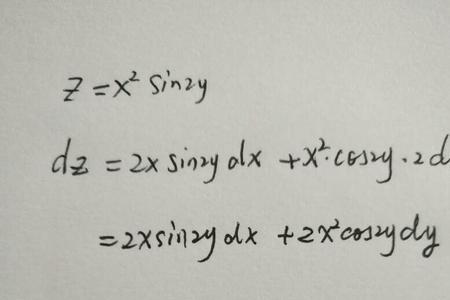sin2α的导数

sin²x求导，sin2x求导，sinx²求导

sin²x=(sinx)²，(sin²x)' = 2sinx·(sinx)'=2sinxcosx=sin2x

(sin2x)' =(cos2x)×2=2cos2x

(sinx²)'=cosx² · (x²)' = 2xcosx²

扩展资料：

复合函数求导的前提：复合函数本身及所含函数都可导。

法则1：设u=g(x)，对f(u)求导得：f'(x)=f'(u)*g'(x)

法则2：设u=g(x)，a=p(u)，对f(a)求导得：f'(x)=f'(a)*p'(u)*g'(x)

常用三角函数求导公式

1、(sinX)'=cosX

2、(cosX)'=-sinX

3、(tanX)'=1/(cosX)2=(secX)2

4、(cotX)'=-1/(sinX)2=-(cscX)2

5、(secX)'=tanX secX

6、(cscX)'=-cotX cscX以上只提供参考

sin2α的导数

二倍角公式 :

sin2α=2sinαcosα tan2α=2tanα/(1-tan^2(α)) cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)。