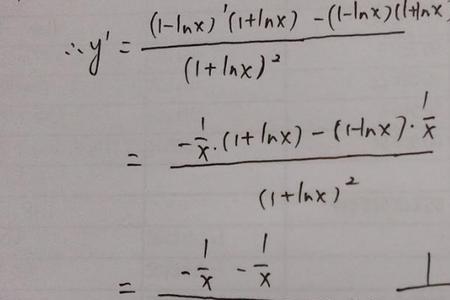lna可以看成一个复合函数
y=lnu u=a
dy/dx=dy/du*du/dx
y'=(lnu)'*u'
=1/u*0 \a是常数,则导数为0
=1/a*0
=0
如果函数y=f(x)的变量x在一点x0上产生增量Δx,函数导出值的增量Δy与变量增量δx的参考值在rx/dx处产生了点x0上的增量Δy。
1、非是全部的函数都是有导数,一个函数也不一定在任何的点上都是有导数。若某函数在某一点导数存有,则称其在这里一点可导,不然称之为不可导。殊不知,可导的函数一定持续不持续的函数一定不可导。
2、对可导的函数f(x),x?f'(x)也是一种导函数,被称为f(x)(通称导数)。找寻已经知道的函数在某点的导数或其导函数的全过程称之为求导数。
本质上,求导数便是一个求极限的全过程,导数的四则运算法则也来自極限的四则运算法则。相反,已经知道导函数还可以相反求原先的函数,即不定积分