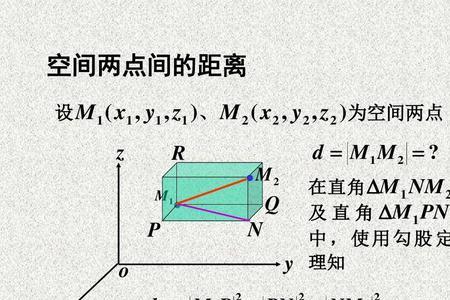
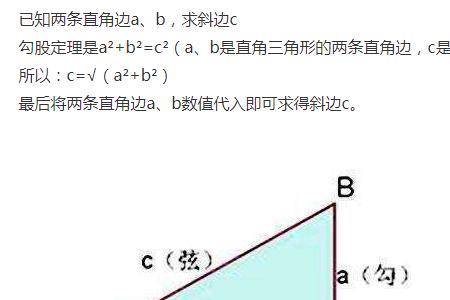
极坐标系的表示方法为P(ρ,θ)。
在极坐标系与平面直角坐标系(笛卡尔坐标系)间转换
极坐标系中的两个坐标 r 和 θ 可以由下面的公式转换为直角坐标系下的坐标值
x=ρcosθ y=ρsinθ
由上述二公式,可得到从直角坐标系中x 和 y 两坐标如何计算出极坐标下的坐标:θ=arctany/x ( x不等于0) 在 x = 0的情况下:若 y 为正数 θ = 90° (π/2 radians)若 y 为负,则 θ = 270° (3π/2radians).
而由直角坐标系引到极坐标系,则公式如下。
r=(x^2+y^2)^0.5。θ则由上述公式逆向求解。