三个正数的算术平均数不小于这三个正数的几何平均数。即a＞0，b＞0，C＞0，（a＋b＋c）／3≥三次根号下abc。它是二元基本不等式延伸。它可看作是a＾3＋b＾3＋C＾3≥3abc。变式而来的。使用三维基本不等式运用条件与二维一致。一正，二定，三等号
基本不等式的3维形式
原创 | 2022-12-05 14:45:27 |浏览：1.6万
猜你想问
-
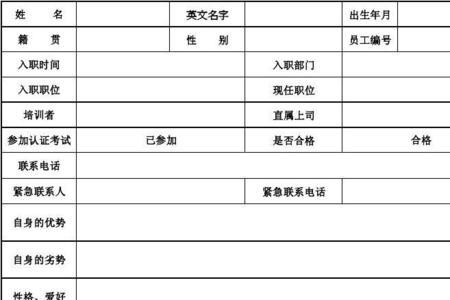了解员工的基本情况都包括什么 包含四方面内容。一是员工个人基础信息。主要是指姓名、性别、出身日期、籍贯、出生地、民族、学历、婚姻、身份证号等信息。二是员工简历信息。包括学习简历和工... -
正反比例的基本条件 正比例的基本条件，例如:速度一定，路程和时间成正比例。路程和时间是两种相关联的量，时间变化路程也随着变化，变化大小和方向相同，且它们的比值一定。反比例条件，例如:`... -
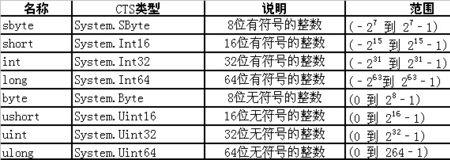c#程序的基本单位 c语言程序的基本单位是函数，函数是C程序的基本组成单位，一个C语言程序中仅有一个main函数，除main函数之外可以有若干个其它的函数，每个函数实现某一特定的操作。其实c... -
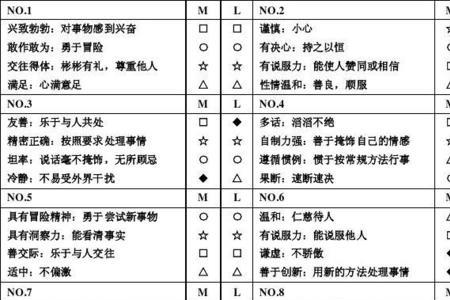人事测评的基本性质是什么 1，人事测评是人员招聘、选拔任用的依据 人事测评的运用可以使人事决策更为科学、准确，并大大提高人员甄选效率。人才选拔的一个关键技术问题是如何预测应聘者在将来... -
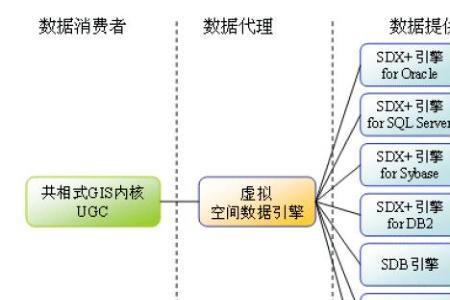gis获取数据的基本方法 GIS的数据获取基本方法就是导入空间数据。空间数据源 ，是指建立GIS的地理数据库所需的各种数据的来源，主要包括地图、遥感图像、文本资料、统计资料、实测数据...
