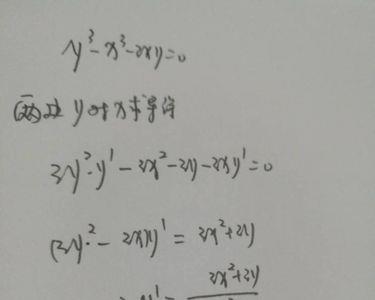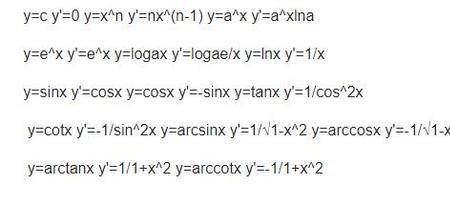y等于x12次方的导数

Y等于X的X次方怎么求导

（x^x）'=(x^x)(lnx+1)

求法：令x^x=y

两边取对数：lny=xlnx

两边求导，应用复合函数求导法则：

(1/y)y'=lnx+1

y'=y(lnx+1)

即：y'=(x^x)(lnx+1)

扩展资料

求导法则：对于一个已经确定存在且可导的情况下，我们可以用复合函数求导的链式法则来进行求导。在方程左右两边都对x进行求导，由于y其实是x的一个函数，所以可以直接得到带有 y' 的一个方程，然后化简得到 y' 的表达式。

隐函数理论的基本问题就是：在适合原方程的一个点的邻近范围内，在函数F(x，y)连续可微的前提下，什么样的附加条件能使得原方程确定一个惟一的函数y=ƒ(x)，不仅单值连续，而且连续可微，其导数由完全确定。隐函数存在定理就用于断定就是这样的一个条件，不仅必要，而且充分。

y等于x12次方的导数

y'=[(½)^x]'=(1/2)^x×ln(1/2)=-ln2/2^x

^表示指数，^x表示x次方。

公式：(a^x)'=(a^x)lna

=(½)的X次方 *ln（1/2） 公式

y=a^x y'=a^xlna

方法一

y=x^x=e^[ln(x^x)]=e^(xlnx)

y'=[e^(xlnx)]'=e^(xlnx)*[(xlnx)]'=e^(xlnx)*[x'lnx+x(lnx)']=e^(xlnx)*[lnx+1']=x^x(1+lnx)

方法二

y=x^x两边取对数

lny=ln(x^x)

lny=xlnx

两边求导

(1/y)*y'=x'lnx+x*(lnx)'

(1/y)*y'=lnx+x*(1/x)

y'=(1+lnx)*y

y'=(1+lnx)*x^x

导数的结果不会因为采取的方法不同而结果不同。

(½)的X次方乘以ln(½)