在经典力学中,时间是标量
在狭义相对论中,坐标时是4-时空矢量的一个分量,固有时是一个标量
在广义相对论中,时空坐标不是矢量,是弯曲空间到闵氏空间的局部同胚,所以坐标时也不是4-矢量的分量,但固有时仍是标量。
坐标时是观测者建立的局域坐标对运动物体的时空曲线的度量,而固有时是运动物体时空曲线的长度。
题主的问题在于认定“矢量(向量)是有长度和方向的量”,实际上这个定义太初等了,连骗高中生我觉得都有点过分。
首先标量也是可以有大小和方向的,方向可以用正负号表示:
有方向的标量包括:电流、电势、时刻
没有方向的标量包括:能量、温度、质量
甚至有的标量可以根据需要决定是否有方向:体积
还有一些物理量可以根据需要成为标量或者矢量:面积
实际上矢量和标量的根本区别在于:
标量可以定义乘法,并且满足一系列规律,标量与矢量可以相乘得到矢量,矢量不能定义乘法,或者定义的乘法不满足标量乘法的一些好的性质。
这些性质包括:封闭性、交换律、结合律、有单位元、除0以外都可逆……
所以究极的定义在这里:
定义1:
设G是一个集合,在G上定义一个运算cdot,它把任意两个G中的元素映射为一个G中的元素,这个运算满足:
1、任何a,b,cin G,满足(acdot b)cdot c=acdot(bcdot c)
2、存在单位元ein G,使得任意ain G
都有ecdot a=acdot e=a
3、任何ain G,存在逆元a^{-1}in G,满足acdot a^{-1}=a^{-1}cdot a=e
那么G叫做一个群。
如果这个运算还满足交换率,即任意a,bin G都有acdot b=bcdot a,这个群叫做一个阿贝尔群。
定义2:
设F是一个集合,在F上定义两个运算,一个叫加法记作+,一个叫乘法记作cdot,满足:
1、F关于加法构成一个阿贝尔群,加法单位元记作0
2、F中所有非0元素关于乘法构成一个阿贝尔群,乘法单位元记作1
3、乘法与加法满足分配律acdot (b+c)=acdot b+acdot c
那么F叫做一个域。
定义3:
设F是一个域,V关于加法+构成一个阿贝尔群,定义一个数乘运算Ftimes Vrightarrow V,满足任意a,bin FX,Yin V
1、a(X+Y)=aX+aY
2、(a+b)X=aX+bX
3、a(bX)=(ab)X
4、1X=X
那么V称为F上的一个线性空间,F中的元素称为标量,V中的元素称为矢量(向量)。
时间是向量吗
时间不是向量。
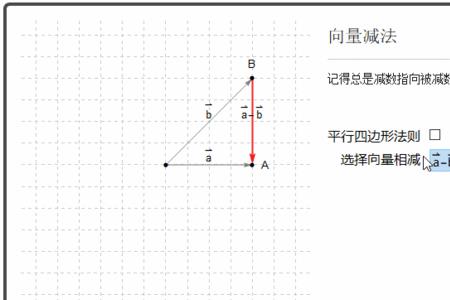
向量(英语:vector,物理、工程等也称作矢量)是数学、物理学和工程科学等多个自然科学中的基本概念。指一个同时具有大小和方向,且满足平行四边形法则的几何对象。