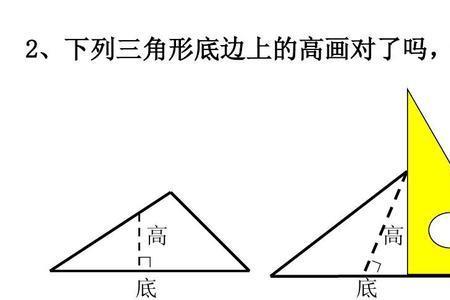
两条直角边都是高,斜边上的高h可以用面积法求得h=直角边边长×另一条直角边边长÷斜边边长。
假设直角三角形ABC中直角边AB的边长为a,直角边AC的边长为b,斜边BC的边长为c,斜边上的高AD为h。
同一个三角形面积相等,所以S=a×b÷2=c×h÷2。
所以,h=a×b÷c,即斜边上的高=直角边边长×另一条直角边边长÷斜边边长
扩展资料
如果斜边的边长是未知量,可以先利用勾股定理求出斜边边长。
斜边边长的平方=直角边的平方+另一条直角边的平方。
然后再利用同一三角形面积相等,求出斜边上的高。
直角三角形的特殊性质:
1、直角三角形两直角边的平方和等于斜边的平方。比如,∠BAC=90°,则AB²+AC²=BC²(勾股定理)。
2、直角三角形中,斜边上的中线等于斜边的一半(即直角三角形的外心位于斜边的中点,外接圆半径R=C/2)。该性质称为直角三角形斜边中线定理。
3、直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。
4、在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半。在直角三角形中,如果有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°。
5、直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。