反正弦函数为什么是有界函数

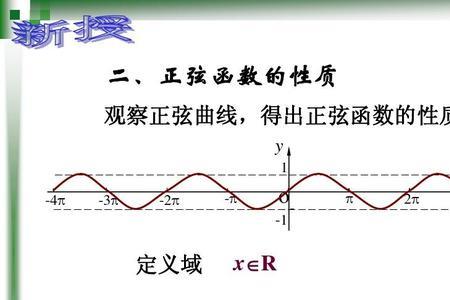
sin cos [-1，1]有界。tg ctg (-无穷，+无穷)无界，上下无限延伸。 反三角函数都是有界的。 由f (x)=sin x所定义的函数f:R → R是有界的。如果正弦函数是定义在所有复数的集合上，则不再是有界的。 函数 （x不等于-1或1）是无界的。

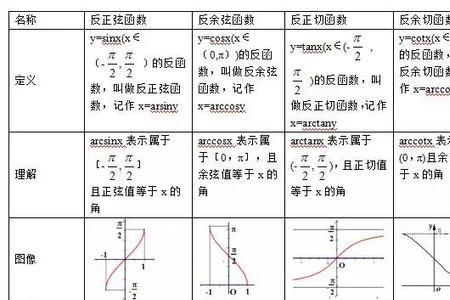
反正弦函数：y=arcsinx ， x属于[-1，1] ， 值域[-ip/2，pi/2]

与函数y= sinx ， x属于[-ip/2，pi/2]的图像关于直线y=x对称

奇函数，在定义域上单调递增 ，所以arcsin(-x) = - arcsinx

反正弦函数为什么是有界函数

反正弦函数是正弦函数在

区间上的反函数，所以反正弦函数有界。

反正弦函数是正弦函数在

区间上的反函数，所以反正弦函数有界。

反正弦函数是正弦函数在

区间上的反函数，所以反正弦函数有界。

反正弦函数是正弦函数在

区间上的反函数，所以反正弦函数有界。