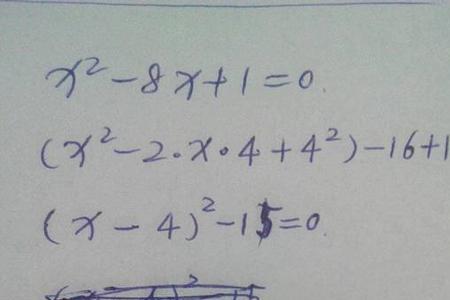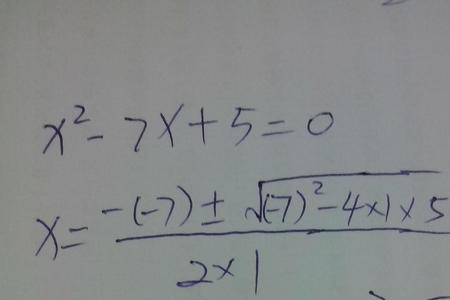通过观察方程会发现此方程可用十字相乘法来分解因式。首先将二次项的系数l,分解成丨乘以丨,分别写在十字交叉线的左上角和左下角,然后将常数项负24分解成负6和4,分别写在十字交叉线的右上角和右下角,最后交叉相乘,把它们的积,相加,看是否等于一次项系数,若不等于一次项系数,从新试验。此时是负6乘以l加上4乘以l,计算得负6加4等于负2,恰好等于一次项的系数。所以x的平方一2x一24=(x一6)(x+4)。
x平方减去2x-24因式分解
X^2一2X一24=(X一6)(X十4)
利用十字相乘法进行分解。
十字相乘法是因式分解中十四种方法之一,另外十三种分别都是:
1、提公因式法
2、公式法
3、双十字相乘法
4、轮换对称法
5、拆添项法
6、配方法
7、因式定理法
8.换元法
9、综合除法
10、主元法
11.特殊值法
12.待定系数法
13.二次多项式。
十字分解法的方法简单来讲就是:十字左边相乘等于二次项,右边相乘等于常数项,交叉相乘再相加等于一次项。其实就是运用乘法公式运算来进行因式分解。