已知行列式值如何求矩阵

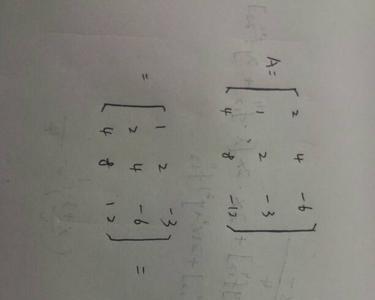
矩阵行列式(determinant of a matrix)是指矩阵的全部元素构成的行列式，设A=(aij)是数域P上的一个n阶矩阵，则所有A=(aij)中的元素组成的行列式称为矩阵A的行列式，记为|A|或det(A)。

若A，B是数域P上的两个n阶矩阵，k是P中的任一个数，则|AB|=|A||B|，|kA|=kn|A|，|A*|=|A|，其中A*是A的伴随矩阵若A是可逆矩阵，则|A|=|A|。

已知行列式值如何求矩阵

公式：|A^T|=|A|，|A^(-1)|=|A|^(-1)，|A*|=|A|^(n-1)，书上都有计算公式，需要记住。|kA|=k^n*|A|