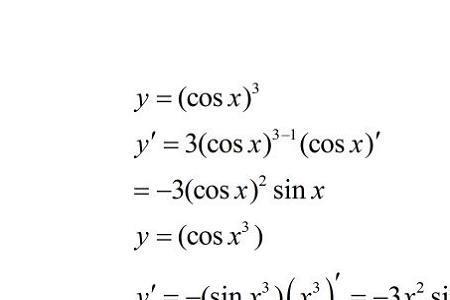√sinx的导数是什么

根号下sinx＝sinx的½次方：

√sinx=（sinx）^1/2

因此，题目转变为求（sinx）^1/2的导数，适用于求导公式（u^v）'=v*u^（v-1）

对u的v次方进行求导，等于v乘以u的v-1次方。

因此，y=（sinx）^1/2

y'=1/2*（sinx）^-1/2

因为x的-1次方等于x（的一次方）分之一，即，x^-1=1/x，以此类推，x的-1/2次方等于x的½次方分之一，即，x^-1/2=1/x^½=1/√x。

所以，y'继续＝1/2*1/√sinx

=1/2√sinx。

√sinx的导数是什么

解：√sinx是y＝x的1／2次方和y＝sinx复合而成的，由复合函数求导方法可知，√sinx的导数＝

cosx／（2√sinx）。