在三角形ABC中a比sinA=a十α+bb比sinA十sinB是成立的,原因在于在任意三角形中都有正弦定理:α:sinA=b:sinB=C:sinC=2R(R为三角形ABC的外接圆的半径。在这个连等式中,我们只要在笫二个等号后面采用比例的性质立即有:α/sinA=b/sinB=(a+b)/(sinA十sinB)。
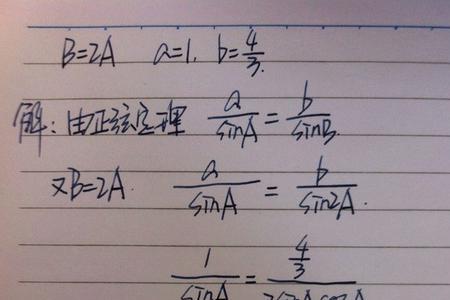
a比sina=a+b比sina+sinb
原创 | 2022-12-05 10:26:00 |浏览:1.6万
猜你想问
-
 NBA比赛胜率如何计算 NBA比赛胜率的计算方式是获胜的场次除以总比赛场次。世界上所有比赛的胜率计算方法都一样。 NBA的排名是按照胜率来排名,不是按照胜负场次多少来排名。 NBA是个高...
NBA比赛胜率如何计算 NBA比赛胜率的计算方式是获胜的场次除以总比赛场次。世界上所有比赛的胜率计算方法都一样。 NBA的排名是按照胜率来排名,不是按照胜负场次多少来排名。 NBA是个高... -
 48v铅酸充电器调到几A比较好 调到2-3a比较好。常用的48V20AH铅酸电瓶电动车充电器,充电电流2-3A,充满电需要8-10小时。48V72AH铅酸电瓶配多大型号的充电器,要根据实际使用情况来决定,如果需要充电...
48v铅酸充电器调到几A比较好 调到2-3a比较好。常用的48V20AH铅酸电瓶电动车充电器,充电电流2-3A,充满电需要8-10小时。48V72AH铅酸电瓶配多大型号的充电器,要根据实际使用情况来决定,如果需要充电... -
 cba比赛规则国际篮联 CBA比赛的规则和国际篮联制订的规则是一样的。为了让中国球员能更好地适应国际篮联规则的变化,使自己能在国际大赛中更好的发挥自己的水平,CBA的比赛一直都是和国际...
cba比赛规则国际篮联 CBA比赛的规则和国际篮联制订的规则是一样的。为了让中国球员能更好地适应国际篮联规则的变化,使自己能在国际大赛中更好的发挥自己的水平,CBA的比赛一直都是和国际... -
 最强nba比卢普斯值得入手吗 最强nba比卢普斯值得入手NBA著名的铁血防守夺得总冠军的,以防守起家立根的平民英雄球队。那时候的比卢普斯是进攻发动机,指挥着全对的进攻。一个优秀篮球智商的后卫...
最强nba比卢普斯值得入手吗 最强nba比卢普斯值得入手NBA著名的铁血防守夺得总冠军的,以防守起家立根的平民英雄球队。那时候的比卢普斯是进攻发动机,指挥着全对的进攻。一个优秀篮球智商的后卫... -
 a比b少百分之几怎么理解 A比b少百分之几代表的意思是b比a数值要大,A只相当于b的一部分。B作为一个标准量。假如a为96,b为100,A比b少4%。我们把b作为标准量,A比b少4%,那么就代表了A相当于b的96%...
a比b少百分之几怎么理解 A比b少百分之几代表的意思是b比a数值要大,A只相当于b的一部分。B作为一个标准量。假如a为96,b为100,A比b少4%。我们把b作为标准量,A比b少4%,那么就代表了A相当于b的96%...
