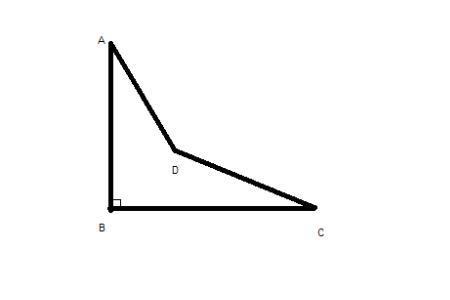
c(斜边)=√(a²+b²)(a,b为两直角边)。
解答过程如下:
(1)在直角三角形中满足勾股定理—在平面上的一个直角三角形中,两个直角边边长的平方加起来等于斜边长的平方。数学表达式:a²+b²=c²。
(2)a²+b²=c²求c,因为c是一条边,所以就是求大于0的一个根。即c=√(a²+b²)。
直角三角形的判定
判定1:有一个角为90°的三角形是直角三角形。
判定2:若a²+b²=c²的平方,则以a、b、c为边的三角形是以c为斜边的直角三角形(勾股定理的逆定理)。
判定3:若一个三角形30°内角所对的边是某一边的一半,那么这个三角形是以这条长边为斜边的直角三角形。
判定4:两个锐角互余的三角形是直角三角形。
判定5:证明直角三角形全等时可以利用HL,两个三角形的斜边长对应相等,以及一个直角边对应相等,则两直角三角形全等。定理:斜边和一条直角对应相等的两个直角三角形全等。
判定6:若两直线相交且它们的斜率之积互为负倒数,则这两直线垂直。
90度角三角形边长公式是怎么样的
直角三角形都满足勾股定理假设直角三角形中两直角边分别为a 、b 斜边为c则a²+b²=c²
直角三角形求各边长计算公式
已知c b边长,求a边长公式
已知c a边长,求b边长公式
已知a b边长,求c边长公式