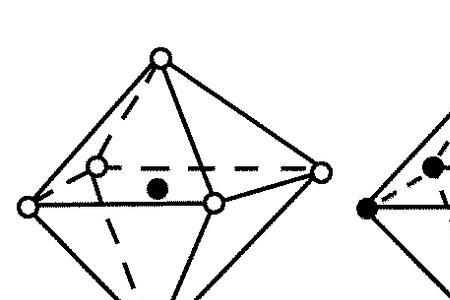
设正四面体P-ABC,底面ABC的高为PO,各棱长为a。
∵PA=PB=PC。
∴OA=OB=OC,(斜线相等,则其射影也相等)。
∴O是正△ABC的外心,(重心)。
延长OA与BC相交于D。
则AD=√3a/2。
根据三角形重心的性质。
AO=2AD/3=√3a/3。
∵△PAO是RT△。
∴根据勾股定理。
PO^2=PA^2-AO^2。
∴PO=√(a^2-a^2/3)= √6a/3。
∴正四面体的高为√6a/3。
正四面体是五种正多面体中的一种,有4个正三角形的面,4个顶点,6条棱。正四面体不同于其它四种正多面体,它没有对称中心。正四面体有六个对称面,其中每一个都通过其一条棱和与这条棱相对的棱的中点。
正四面体很容易由正方体得到,只要从正方体一个顶点A引三个面的对角线AB,AC,AD,并两点两点连结之即可。正四面体和一般四面体一样,根据保利克-施瓦兹定理能够用空间四边形及其对角线表示。正四面体的对偶是其自身。