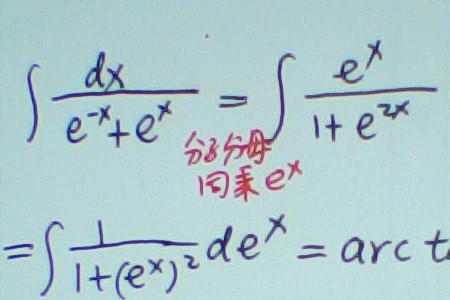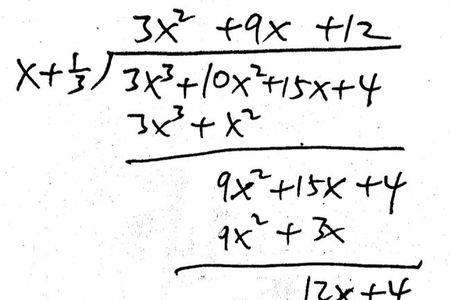辗转相除法应用的前提是(x,y)=z
所以z整除mx+ny (m,n∈Z)
x/y=a…b 既x—ay=b
因为z整除x—ay
所以z整除b
也就是说照两个特别大的数的最小公约数就互除就可以了,除到两个非常小的数找它们的最小公约数,和两个大数是一样的,它们互质两个大数也互质。
更相减损法也是一样的,只不过更特殊一点,就是上头的m,n分别都是1的情况,但是原理是一样的。
举个例子。
542x+245y=1
(542,245)=(52,245)=(52,37)=(15,37)=(15,7)=1
反过来写1=15-2*7
=15-2*(37-2*15)=15*5-2*37
=5*(52-37)-2*37
=5*52-7*(245-4*52)=33*52-7*245
=33*(542-2*245)-7*245
=33*542-73*245
得到一组解
33和—73
所有解就是
x=33+245t
y=—73—542t
不过解ax+by=c有整数解重要条件是(a
b)整除c,不然还得约。
比如143x—77y=187
就等价于13x—7y=17
这样去解。