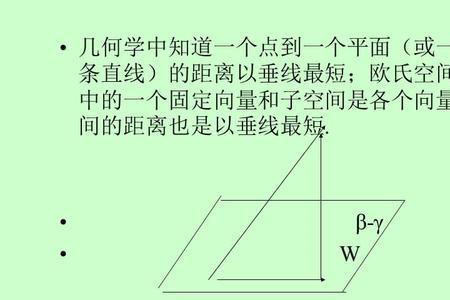
这里应是直线与平面平行。取平面内任意一点A与直线上任意一点B得向量AB。平面法向量为n。则直线到平面距离d=n点乘AB/lnl。即向量AB在法向量n上投影。与平面外一点到平面距离公式是一致的。此公式可引申到空间异面直线间距离。A,B分别是两异面直线各取一点。法向量与两异面直线同时垂垂直。
空间向量直线到平面的距离
设直线行于平面.平面的法向量为n.
a为直线上的任意一点,b为平面上的任意一点.
则,直线到这平面的距离d,即等于向量ab在向量n上的投影的绝对值.
即:d=|n点乘ab|/|n|.
如果乐意,自然可换成坐标表达式.
设直线行于平面.平面的法向量为n.
A为直线上的任意一点,B为平面上的任意一点.
则,直线到这平面的距离d,即等于向量AB在向量n上的投影的绝对值.
即:d=|n点乘AB|/|n|.