一、sin度数公式
1、sin 30= 1/2
2、sin 45=根号2/2
3、sin 60= 根号3/2
二、cos度数公式
1、cos 30=根号3/2
2、cos 45=根号2/2
3、cos 60=1/2
三、tan度数公式
1、tan 30=根号3/3
2、tan 45=1
3、tan 60=根号3
扩展资料:
常见的三角函数包括正弦函数、余弦函数和正切函数。在航海学、测绘学、工程学等其他学科中,还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。
早期对于三角函数的研究可以追溯到古代。古希腊三角术的奠基人是公元前2世纪的喜帕恰斯。他按照古巴比伦人的做法,将圆周分为360等份(即圆周的弧度为360度,与现代的弧度制不同)。对于给定的弧度,他给出了对应的弦的长度数值,这个记法和现代的正弦函数是等价的。
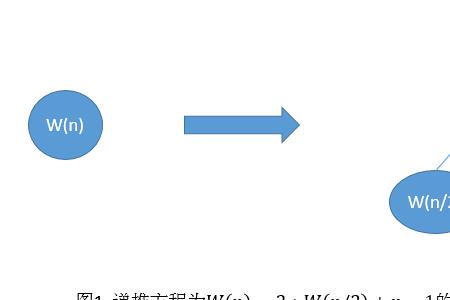
树求度数的3个公式
二叉树是树形结构中一种特殊的树形结构,二叉树中的每个结点至多有2棵子树,节点度数:节点子节点的个数
二叉树度数:所有节点度数取最大值
二叉树的度小于等于2,因为二叉树的定义要求二叉树中任意结点的度数(结点的分支数)小于等于2,假设二叉树的节点数为n,总边数为m,度为0的节点个数为n0,度为1的节点个数为n1,度为2的节点个数为n2,那么很容易有下列公式:
总节点数: n = n 0 + n 1 + n 2 n=n_0+n_1+n_2 n=n0+n1+n2
总边数: m = n − 1 m=n-1 m=n−1
总边数: m = 2 ∗ n 2 + 1 ∗ n 1 + 0 ∗ n 0 m=2*n_2 + 1*n_1 + 0*n_0 m=2∗n2+1∗n1+0∗n0
树求度数的3个公式
1、节点的度与树的度
节点的度:结点拥有的子树数目称为结点的度,叶子结点 就是度为0的结点
树的度:树内各结点的度的最大值
分支节点:度不为0的节点
--------------------------------------------------
节点数n=n0+n1+n2, ( n0:度为0的结点数,n1:度为1的结点 n2:度为2的结点数。 n是总结点)
非空二叉树,n0=n2+1
当节点数n为奇数,无度为1的节点节点n为偶数,有一个度为1的节点
--------------------------------------------------
分支数=n-1 =1*n1+ 2*n2+3*n3
n0+n1+n2+n3 = n = 分支数+1 = 1*n1+ 2*n2+3*n3+1
2、树的深度与高度
节点 ni 的深度:从根节点到 ni 的的唯一路径长。即,节点 ni 所在的层次(根节点为0层),树的深度 = 树中节点的最大层次。
节点 ni 的高度:从 ni 到一片树叶的最长路径长。即,叶子节点的高度为0,树的高度 = 根的高度。
树的深度 = 树的高度
高度为h的二叉树至少2^h个节点,至多有2^(h+1)-1 个节点。
含有n≥1 个节点的二叉树的高度范围:[ | log2 n」,n-1]
3、完全二叉树:
只有最下面的两层结点度小于2,并且最下面一层的结点都集中在该层最左边的若干位置。
有 n 个节点的完全二叉树的高度(深度)为 | log2 n」
完全二叉树第 n 层上至多 2^(n+1)个节点
完全二叉树第 n 层上节点编号: 2^n - 2^(n+1)-1
--------------------------------------------------
例1:在一棵具有n个结点的完全二叉树中,树枝结点的最大编号为( B ).假定树根结点的编号为1
A.(n-1)/2 B.n/2 C.n/2-1
例2:编号13的左兄弟节点是( A ),右兄弟节点是( B )
A.12 B.14
层数 = | log2 n」= 3
3层编号范围 8-15
例3:若一棵完全二叉树有768 个结点,则该二叉树中叶结点的个数是( C )。
A.257 B.258 C.384 D.385
n=n0+n1+n2
当节点数n为奇数,无度为1的节点节点n为偶数,有一个度为1的节点,n1 = 1
768=n0+n1+n2n2=n0-1
所以n0=384
例4:一颗完全二叉树第六层有8个叶结点(根为第一层),则结点个数最多有()个。
正确答案: D 你的答案: B (错误)
A.39 B.72 C.104 D.111
二叉树第k层最多有2的(k-1)次方个节点
1-6层 : 2^6-1=63个
7 层: 24*2 = 48 第七层的节点是第六层的左边24个的子节点(因为最右边8个是叶子节点),所以是48个
所以,63+ 48 = 111
例5:将一棵有100个结点的完全二叉树从根这一层开始,开始进行层次遍历编号,那么编号最小的叶节点的编号为(根节点为1)
正确答案: C 你的答案: A (错误)
49 50 51 52
解析1:完全二叉树中,对于编号为i的父结点,左孩子编号为2*i',右孩子编号为2*i+1
编号为100的节点对应的父节点编号为50,故最小叶子节点编号为51
解析2:深度为6的满二叉树的节点数为 2^6 - 1 = 63
深度为7的满二叉书的节点数为 2^7 - 1 = 127
因此含有100个节点的完全二叉树的深度为7,叶子节点分布在第6层和第7层。
第七层叶子节点数为:100 - 63 = 37
37 / 2 = 18余1
因此,第6层的前18个节点是2度节点,第19个节点是1度节点即只有左子树,没有右子树,即第6层前19个节点为非叶子节点,之后为叶子节点。
因此编号最小的叶子节点编号为:2 ^5 - 1 + 19 + 1 = 51.
其中,2^5 - 1位前5层非叶子节点数(由满二叉树的节点计算公式得出)
4、满二叉树:
是一颗完全二叉树除了叶结点外每一个结点都有左右子叶且叶结点都处在最底层。
第 n 层有 2^(n+1)-1 个节点
深度为k,且有 2^(k+1)-1个节点。
5、堆:
是一颗完全二叉树
大顶堆:左右子树的结点值都小于根结点值,左右子树都是大顶堆。
小顶堆:左右子树的结点值都大于根结点值,左右子树都是小顶堆。
6、二叉排序树(二叉查找树):
左子树上的值都小于根结点的值,右子树上的值都大于根结点得值,左右子树都是二叉排序树。
例:将整数序列(7-2-4-6-3-1-5)按所示顺序构建一棵二叉排序树a(亦称二叉搜索树),之后将整数8按照二叉排序树规则插入树a中,请问插入之后的树a中序遍历结果是____。
正确答案: A 你的答案: A (正确)
A.1-2-3-4-5-6-7-8 B.7-2-1-4-3-6-5-8 C.1-3-5-2-4-6-7-8
D.1-3-5-6-4-2-8-7 E.7-2-8-1-4-3-6-5 F.5-6-3-4-1-2-7-8
不用看题目直接看答案排除,二叉排序树的中序遍历一定有序
7
2
8
1
4
3
6
5
例:假设某棵二叉查找树的所有键均为1到10的整数,现在我们要查找5。下面____不可能是键的检查序列。
A.10,9,8,7,6,5 B.2,8,6,3,7,4,5 C.1,2,9,3,8,7,4,6,5 D.2,3,10,4,8,5 E.4,9,8,7,5 F.以上均正确
7、平衡二叉树(ALV):
是一颗二叉排序树左子树和右子树的高度差值不超过1,左右子树都为平衡二叉树。
插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)
插入操作:在平衡二叉树中插入结点与二叉查找树最大的不同在于要随时保证插入后整棵二叉树是平衡的。那么调整不平衡树的基本方法就是: 旋转,基本思路都是转换到左旋和右旋。
1) 右旋: 在最小平衡子树根节点平衡因子>=2且在根节点的左孩子的左孩子插入元素,进行右旋
2) 左旋: 在最小平衡子树根节点平衡因子>=-2且在根节点的右孩子的右孩子插入元素,进行左旋。
3) 右左:最小平衡子树根节点(80)的右孩子(100)的左孩子(90)的子节点(95)插入新元素,先绕根节点的右孩子节点(100)右旋,再围根节点(80)左旋
4) 左右:在最小平衡子树根节点(80)的左孩子(50)的右孩子(70)的子节点插入新元素,先绕根节点的左孩子节点(50)右旋,再围根节点(80)左旋
8、红黑树:
与AVL类似,平衡二叉B树,并不追求“完全平衡”——它只要求部分地达到平衡要求,降低了对旋转的要求,从而提高了性能。
红黑树的算法时间复杂度和AVL相同
红黑树的特性:
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
注意:
(特性(3)中的叶子节点,是只为空(NIL或null)的节点。
特性(5),确保没有一条路径会比其他路径长出俩倍。因而,红黑树是相对是接近平衡的二叉树。
根据被插入节点的父节点的情况,可以将"当节点z被着色为红色节点,并插入二叉树"划分为三种情况来处理。
① 情况说明:被插入的节点是根节点。
处理方法:直接把此节点涂为黑色。
② 情况说明:被插入的节点的父节点是黑色。
处理方法:什么也不需要做。节点被插入后,仍然是红黑树。
③ 情况说明:被插入的节点的父节点是红色。
处理方法:那么,该情况与红黑树的“特性(5)”相冲突。这种情况下,被插入节点是一定存在非空祖父节点的进一步的讲,被插入节点也一定存在叔叔节点(即使叔叔节点为空,我们也视之为存在,空节点本身就是黑色节点)。理解这点之后,我们依据"叔叔节点的情况",将这种情况进一步划分为3种情况(Case)。
现象说明
处理策略
Case 1
当前节点的父节点是红色,且当前节点的祖父节点的另一个子节点(叔叔节点)也是红色。
(01) 将“父节点”设为黑色。
(02) 将“叔叔节点”设为黑色。
(03) 将“祖父节点”设为“红色”。
(04) 将“祖父节点”设为“当前节点”(红色节点)即,之后继续对“当前节点”进行操作。
Case 2
当前节点的父节点是红色,叔叔节点是黑色,且当前节点是其父节点的右孩子
(01) 将“父节点”作为“新的当前节点”。
(02) 以“新的当前节点”为支点进行左旋。
Case 3
当前节点的父节点是红色,叔叔节点是黑色,且当前节点是其父节点的左孩子
(01) 将“父节点”设为“黑色”。
(02) 将“祖父节点”设为“红色”。
(03) 以“祖父节点”为支点进行右旋。
上面三种情况(Case)处理问题的核心思路都是:将红色的节点移到根节点然后,将根节点设为黑色。下面对它们详细进行介绍。
红黑树的应用
红黑树的应用比较广泛,主要是用它来存储有序的数据,它的时间复杂度是O(lgn),效率非常之高。
例如,Java集合中的TreeSet和TreeMap,C++ STL中的set、map,以及Linux虚拟内存的管理,都是通过红黑树去实现的。
2-3-4树
2-3-4树和红黑树一样,也是平衡树。只不过不是二叉树,它的子节点数目可以达到4个。
每个节点存储的数据项可以达到3个。名字中的2,3,4是指节点可能包含的子节点数目。具体而言:
1、若父节点中存有1个数据项,则必有2个子节点。
2、若父节点中存有2个数据项,则必有3个子节点。
3、若父节点中存有3个数据项,则必有4个子节点。
也就是说子节点的数目是父节点中数据项的数目加一。因为以上三个规则,使得除了叶结点外,其他节点必有2到4个子节点,不可能只有一个子节点。所以不叫1-2-3-4树。而且2-3-4树中所有叶结点总是在同一层。
9、B树:
是一种多路搜索树(并不是二叉的):
1.定义任意非叶子结点最多只有M个儿子且M>2
2.根结点的儿子数为[2, M]
3.除根结点以外的非叶子结点的儿子数为[M/2, M]
4.每个结点存放至少M/2-1(取上整)和至多M-1个关键字(至少2个关键字)
5.非叶子结点的关键字个数=指向儿子的指针个数-1
6.非叶子结点的关键字:K[1], K[2], …, K[M-1]且K[i] < K[i+1]
7.非叶子结点的指针:P[1], P[2], …, P[M]其中P[1]指向关键字小于K[1]的
子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树
8.所有叶子结点位于同一层
如:(M=3)
B-树的特性:
1.关键字集合分布在整颗树中
2.任何一个关键字出现且只出现在一个结点中
3.搜索有可能在非叶子结点结束
4.其搜索性能等价于在关键字全集内做一次二分查找
5.自动层次控制
由于限制了除根结点以外的非叶子结点,至少含有M/2个儿子,确保了结点的至少
利用率,其