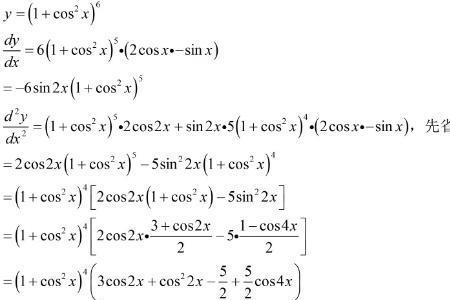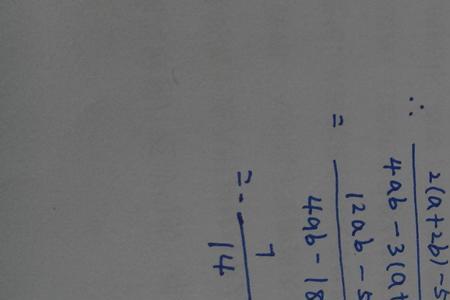x的负二次方的导数是

x求导为1，2是常数，求导后为0，所以x-2求导后为1。

当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'（x0）或df（x0）/dx。

使用方法：

一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。

x的负二次方的导数是

函数y=(1/x)²是一个分式函数，它的自变量的取值范围是非零实数，它的值域是正实数，那么它的导数是多少呢?对于y=1/x²，我们可以利用分式求导的公式进行求解，那么，我们知道它等于-2x/x的4次方，也就是-2/x³也可以对y=(1/x)²利用复合函数求导，其结果也是-2/x³。

x的负二次方的导数是

对于任意实数a，幂函数y = x^a为可导函数，其导数dy/dx = ax^(a-1)

所以y = x^(-2)的导数为y' = -2x^(-3)