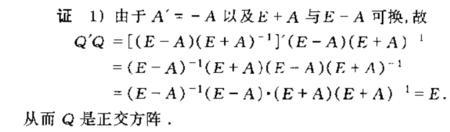(a+b)(a-b)=a²-ab+ba-b²=a²-b²,由此可见,数字的平方差公式(a+b)(a-b)=a²-b²之所以存在,是因为
-ab+ba=0,即ab=ba,这是因为数字的乘积满足交换律。所以是否满足交换律是平方差公式能否成立的基础。
对于矩阵,设有矩阵A和矩阵B,一般的,即使AB有意义,BA也可能根本就没意义。即使AB和BA都有意义,两者也未必相等。哪怕在AB是行列数相同的矩阵,一般来说也是AB≠BA。那么(A+B)(A-B)=A²-AB+BA-B²≠A²-B²。所以矩阵没有平方差公式。
事实上对于矩阵,同样(A+B)²≠A²+2AB+B²。
矩阵平方差公式满足吗
矩阵平方差公式满足的充要条件是方阵A和B满足:AB=BA。
【证明】
(A+B)(A-B)
=AA+BA-AB-BB
=A²+BA-AB-B²
∴(A+B)(A-B)=A²-B²
的充要条件是
AB=BA