两直线平行的性质 直线方程

在平面上两条直线、空间的两个平面以及空间的一条直线与一平面之间没有任何公共点时，称它们平行。两直线平行的公式：A2B1=A1B2，即：A1B2-A2B1=0。

两直线平行公式是什么

根据直线方程的一般式判断两直线平行

若直线L1:A1x+B1y+C1=0与直线L2:A2x+B2y+C2=0

①若B1=B2=0，此时两直线斜率不存在，满足:A1/A1=B1/B2≠C1/C2

②若B1≠0、B2≠0，此时也满足A1/A2=B1/B2≠C1/C2。

则有两条直线平行，有A1/A2=B1/B2≠C1/C2。

平行的性质

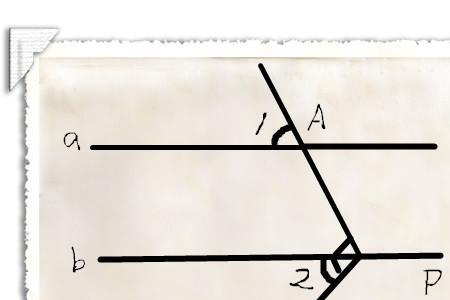
（1）两条平行线被第三条直线所截，同旁内角互补（简称“两直线平行，同旁内角互补”）。

（2）两条平行线被第三条直线所截，内错角相等（简称“两直线平行，内错角相等”）。

（3）两条平行线被第三条直线所截，同位角相等（简称“两直线平行，同位角相等”）。

（4）经过直线外一点有且只有一条直线与这条直线平行（平行公理）。

（5）若两条直线分别与另一条直线互相平行，则这两条直线也互相平行。

（6）平行线间的距离处处相等

两直线平行的性质 直线方程

直线方程一般式:ax+by+c=0

斜截式(斜率存在):y=kx+b

k=-a/b

两直线平行的条件是斜率相等，即k1=k2

一般式是: a1:a2=b1:b2不等于c1:c2 。

如果两条直线有斜率，且L1//L2，则斜率相等，截距不等。

即L1:y=k1x+b1，L2:y=k2x+b2，L1//L2，则k1=k2，b1≠b2

若L1⊥L2，且两条直线有斜率，则斜率之积为-1，即k1k2=-1.

两直线平行的性质 直线方程

两条平行线被第三条直线所截，同位角相等，内错角相等，同旁内角互补。

两直线平行的判定定理：

1、两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行如果内错角相等。那么这两条直线平行如果同旁内角互补，那么这两条直线平行。

这三个条件都是由角的数量关系（相等或互补）来确定直线的位置关系（平行）的，因此能否找到两直线平行的条件，关键是能否正确地找到或识别出同位角，内错角或同旁内角。

2、如果两条直线都与第三条直线平行，那么这两条直线互相平行，即平行于同一直线的二直线平行。

3、同一平面内，垂直于同一直线的二直线互相平行 。

扩展资料

平行线的平行公理：

1、经过直线外一点，有且只有一条直线与已知直线平行。

2、两条平行线被第三条直线所截，同位角相等，内错角相等，同旁内角互补。

注意：只有两条平行线被第三条直线所截，同位角才会相等，内错角相等 同旁内角互补