三角形已知两边求面积公式

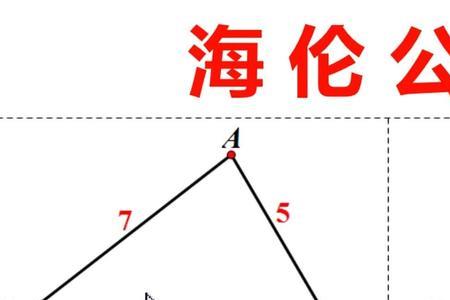
已知三角形两边a，b，这两边夹角C，则S=1/2

absinC，即两夹边之积乘夹角的正弦值。

各类三角形求面积方式如下所示：

1、已知三角形底a，高h，则 S=ah/2

2、已知三角形三边a，b，c，则

（海伦公式）（p=(a+b+c)/2）

S=sqrt[p(p-a)(p-b)(p-c)]

=sqrt[(1/16)(a+b+c)(a+b-c)(a+c-b)(b+c-a)]

=1/4sqrt[(a+b+c)(a+b-c)(a+c-b)(b+c-a)]

3、已知三角形两边a，b，这两边夹角C，则S=1/2

absinC，即两夹边之积乘夹角的正弦值。

4、设三角形三边分别为a、b、c，内切圆半径为r

则三角形面积=(a+b+c)r/2

5、设三角形三边分别为a、b、c，外接圆半径为R

则三角形面积=abc/4R

6、行列式形式

为三阶行列式，此三角形

在平面直角坐标系内

三角形已知两边求面积公式

面积等于两边之积得二分之一乘以这两边夹角的正弦。

即：S△ABC=1/2AB*BC*sin∠B

已知两边a，b所以夹角的cosC值可以求出，利用sinC^2+cosC^2=1，可以求出sinC的值，在按公式S=1/2a*b*sinC

少一个条件。应该是知道这两边夹的角是多少度。如果设这两边分边为a、b。两边的夹角是C.

那么。S=（1/2）ab*SinC

三角形已知两边求面积公式

少一个条件。应该是知道这两边夹的角是多少度。如果设这两边分边为a、b。两边的夹角是C.那么。S=（1/2）ab*SinC